八年级数学 第一学期第二次阶段性测试
第一学期第二次阶段性测试
试卷
考查范围:第12章至16章菱形 出卷:洪 澄 审核:初二数学备课组
亲爱的同学:
祝贺你完成了一个阶段的学习,通过这一阶段的学习,你一定发现了数学和我们的生活联系紧密,学数学很好玩,也很有趣;现在是展示你的学习成果的时候了,你可以尽情地发挥,祝你成功!
本试卷满分100分,在90分钟内完成,要细心,相信你,你是最好的!
一、耐心填一填(每空2分,共32分)
1、16的算术平方根是 , 的立方根是-3。
 2、
2、 ![]() ·
·![]() =___ _; 32a2b2c÷4ab=_______;若
=___ _; 32a2b2c÷4ab=_______;若![]() =16,则 m=________.
=16,则 m=________.
3、若 ![]() 则
则![]()
|
5、在□ABCD中,如果∠A+∠C=100°,则∠B=_____°
6、菱形ABCD的两条对角线的长分别为6cm、8cm,则菱形ABCD的周长为_______cm,面积为_____________cm2
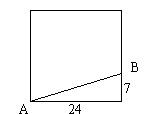
 7、某洗衣机的包装箱外形是长方体,其高为1.2m,体积为1.2m3,底面是正方形,则该包装箱的表面积为 m2。
7、某洗衣机的包装箱外形是长方体,其高为1.2m,体积为1.2m3,底面是正方形,则该包装箱的表面积为 m2。
|
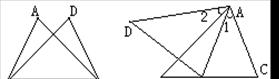
9、如图3,∠ABC=∠DCB,请补充一个条件: ,使△ABC≌△DCB.
如图4,∠1=∠2,AD=AB,请补充一个条件: ,使△ABC≌△ADE.
|
|
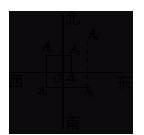
10、如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点。按如此规律走下去,当机器人走到A6点时,离O点的距离是 米.
二、精心选一选(每小题3分,共24分)
11、在,,–3.1416 ,π,,0.……,中无理数有 ( )
A.2个 B.3个 C.4个 D.5个
12、下列计算正确的是( )
A.a6÷a3=a2 B.(a-1)2=a2-2a+1
C.(3a)2=6a2 D.(a3)2=a5
13、矩形具有而菱形不一定具有的性质是( )
 A.对角线互相平分
B.对角相等
A.对角线互相平分
B.对角相等
C.四个内角都相等 D.对角线互相垂直
14、如图,平行四边形 ABCD的对角线AC、BD相交于点O,
则图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
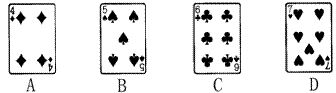
15、如图,给出的四张扑克牌,请你先闭上眼睛,这时小明同学将其中一张旋转1800并告诉你:此张旋转前后完全不变,然后让你张眼辨认,小明旋转的一张扑克牌是 ( )

|
 OE⊥AC交AD于E,则△DCE的周长为 (
)
OE⊥AC交AD于E,则△DCE的周长为 (
)
A.4 cm B.6cm C.8cm D.10cm
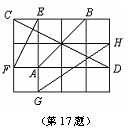
17、如图,每个小正方形的边长是1,图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A. CD、EF、GH B. AB、EF、GH
C. AB、CD、GH D. AB、CD、EF
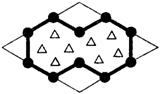 18、如图,菱形花坛的边长为6cm,一个内角为60℃,在花坛中用花盆围出两个正六边形的图形(图中粗线部分),则围出的图形的周长为( )
18、如图,菱形花坛的边长为6cm,一个内角为60℃,在花坛中用花盆围出两个正六边形的图形(图中粗线部分),则围出的图形的周长为( )
A.20cm B.22cm C.24cm D.以上都不对
|
19.计算(第1至4小题每题3分,第5至6小题每题4分,共20分.)
(1)-12x3y4÷(-3x2y3)·(-![]() xy)
(2)(2x+1)(2x-3)
xy)
(2)(2x+1)(2x-3)
(3) (2a+1)2(2a-1)2; (4) (2x-y-1)(2x-y+1);
(5) 若x、y都是实数,且y=![]() +
+![]() +8,求x+3y的立方根.
+8,求x+3y的立方根.
(6)如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如: 4=22-02
![]() ,
,
![]() ,
,
因此4,12,20都是“神秘数”
①44是“神秘数”吗?为什么?
②设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
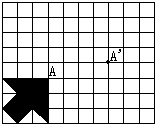 20、实践与操作(3分+6分)
20、实践与操作(3分+6分)
(1)如图,平移方格纸中的图形,使点A平移到点A'处,画出平移后的图形.
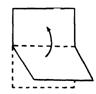
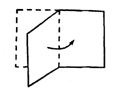
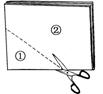
(2)将一张矩形纸对折再对折,然后沿着图中的虚线剪下(如图甲),得到①、②两部分,将①展开成图乙中的四边形ABCD。
 | |||||||
 |  | ||||||
 | |||||||
|
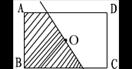
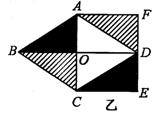
(1)四边形ABCD是什么四边形?根据的数学道理是什么?
(2)将四边形ABCD沿对角线AC、BD剪开,然后将△BOC平移到右上方△ADF处,将△ABO平移到右下方△CDE处,所拼成的四边形ACEF是什么图形?说明理由。
21、说理与证明(6分+4分+6分)
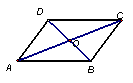
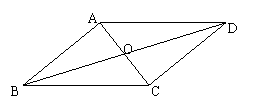
(1)如图,四边形ABCD是平行四边形,对角线AC、BD相交于O。
①如果∠ABC = 40º,求∠ADC,∠BCD的度数。
②如果AD=20,AC=18,BD=26,求△OBC的周长。
③如果AB=10,AO=6,BO=8,这个平行四边形是菱形吗?为什么?
 |
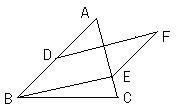
(2)如图,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE
①猜想:DF和AE间的关系是 。
②说明你的道理。
(3)已知:如图,在□ABCD 中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
①求证:△ADE≌△CBF;
②若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
 |
友情提示:请同学们做完后仔细的检查一下,祝你考出好成绩。