八年级第二学期期末考试数学试题

八年级第二学期期末考试数学试题

题号	一	二	三	四	五	六	总分
得分

一．选择题 （每题2分，共20分）

1.在实数π，－cos60°，0.……，，中，有理数有（　　　）.

A.2个　　　　　 B.3个　　　　　  C.4个　　　　　 D.5个

2．如果=5-x那么（　　　 ）.

A.ｘ＞０　　　　 B.ｘ５　　　　  C.不存在　　　　 D.以上都不对

3.在直角坐标系中，点P（-3，5）关于y轴对称的点的坐标是（　　　 ）.

A．（3，5）　　　 B．（3，-5）　　  C．（-3，5）　　 D．（-3，-5）

4.在比例尺为1：10000的地图上，1cm 的区域的实际面积是（　　　 ）.

A.10m　　　　  B.100 m　　　　 C.1000 m　　  D.10000 m

5.在等腰△ABC和等腰△DEF中，∠A与∠D是顶角，下列判断正确的是（　　　 ）.

①∠A=∠D时，两三角形相似；　　　　②∠A=∠E时，两三角形相似；

③=时，两三角形相似；　　　④∠B=∠E时，两三角形相似。

A.1个　　　　　  B.2个　　　　　  C.3个　　　　　  D.4个

6.在△ABC中，∠A：∠B：∠C＝1：2：3，则tanA+cosB等于（　　　 ）.

A.　　　 B.　　　　C. 　　　　D.

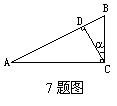
7.如图Rt△ABC中，∠ACB=90º，CD⊥AB于D，BC=3，AC=4，设∠BCD=a， 则tana的值为（　　 　）.

A. 　　　　　 B. 　　　　 C. 　　　　　 D.

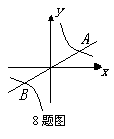
8.如图所示，直线与双曲线y=的一个交点A的坐标为（3，2），则它的另一个交点B的坐标为（　　  ）.

　A.（2，3）　　　　B.（-2，-3）　　　　 C.（-3，-2）　　　　  D.（-4，-3）

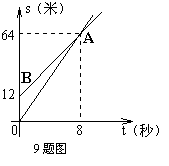
9.如图，OA，BA分别表示甲、乙两名学生运动的一次函数图象， 图中s和t分别表示运动路程和时间，根据图象判断快者的速度比慢者的速度每秒快（　　　）.

A.2.5米　　　　  B.2米　　　　　　　  C.1.5米　　　　　　　 D.1米

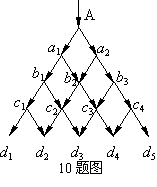
10.一条信息可以通过如图所示的网络由上（A点）往下向各站传送，如信息b₂可由经a₁的站点送达，也可由经a₂的站点送达，共有两条途径传送，则信息由A点到d₃的不同途径共有（　　 ）

A.3条　　　　　  B.4条　　　　　　　  C.6条　　　　　　　  D.12条

二、填空题（每题3，共27分）

11.两个相似三角形周长比为1︰4,则其对应边上的高的比为　　　　　　 .

12.据天气预报，某地今天的最低气温23℃，最高气温34℃，则今天该地的气温极差为　　　　.

13.若点（２＋ａ，２ａ＋３）在第四象限，则ａ的取值是　　　　　　.

14.直角三角形的斜边与斜边上的中线的比是　　　　 .

15.已知函数的图像经过（２，－４），（－２，４）两点，请写出满足上述条件的两个不同的函数的解析式　　　　　　　　　　　、　　　　　　　　　　　　　。

16.点A（x₁，y₁），B（x₂，y₂）是反比例函数y=的图象上两点，若0＜x₁＜x₂，则y_1、、

y₂的大小关系是　　　　　  .

17.小辉沿着坡度ｉ＝１：的梯子向上走３０米，这时她离地面的高度是　　　　米.

18.袋中有红、黄、蓝3球，从中摸出一个，放回，共摸3次，摸到二黄一蓝的机会是　　  .

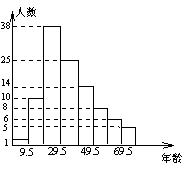
19.2003年，国家卫生部信息统计中心根据国务院新闻办公室授权发布全国内地5月21日至5月25日非典型肺炎发病情况，按年龄段进行统计分析中，各年龄段发病的总人数如图所示。观察图形你能获得哪些信息（至少写三条）：　　　　　　　　　　　　　　　　 　　　　　　　

　　　　　　 　　　　　　　　　　　　　　.

三、计算或化简（20题8分，21题4分，共12分）

20.（1） +  +-　　  （2） sin60°×cos45°+tan37ºcot37º

21.八年级一、二班举行投篮比赛，每班各挑选10名同学代表班级参加7轮积分赛，投篮命中率如下：

场次	1	2	3	4	5	6	7
一班	85%	88%	77%	75%	85%	80%	70%
二班	90%	85%	70%	80%	60%	83%	92%

你认为哪个班级的投篮命中率较稳定？为什么？

四、实验操作（22题4分，21题6分，共10分）

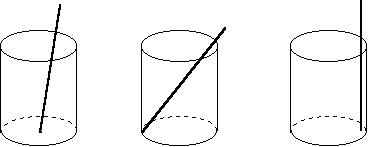
22.将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，如图，设筷子露出在杯子外面长为hcm，则h的取值范围是什么？

23.将长为38cm，宽为5cm的长方形白纸，按如图所示方法粘合在一起，粘合部分白纸为2cm。

(1)求10张白纸粘合后的长度；

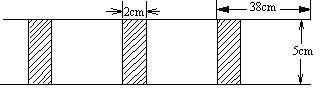(2)设x张白纸粘合后的总长为ycm，写出y与x的函数关系式。

五、应用题（24题7分，25题8分，共15分）

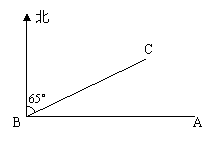24.A市气象发报，一沙尘暴中心在A市正西方向1000Km的B处，正迅速向北偏东65°的方向沿BC移动，距沙尘暴400Km范围内为受沙尘暴影响区域，请你用学过知识说明A市是否受沙尘暴影响？

25.已知小山的高为h，为了测量小山顶上铁塔AB的高x，在平地上选择一点P，在P点处测得B点的仰角为α，A点的仰角为β.（如图）

（1）试用α、β和h的关系式表示铁塔的高x；

（2）在表中根据第一次和第二次的“测得数据”，填写“平均值”一列中α、β的数值；

已知数据	山高BC	h=153.48m
测 得 数 据	测量项目		第一次	第二次	平均值
	仰角α		29°17′	29°19′	α=　　.
	仰角β		34°01′	33°57′	β=　　.

（3）根据表中数据求出铁塔高x的值（精确到0.01m）.

六、解答题（从以下三题中任选两题解答，共16分）

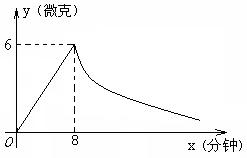26.（8分）为了预防“传染病”，某学校对教师采用药熏消毒法进行消毒.已知药物燃烧时，室内每立方米空气中的含药量y（微克）与时间x（分钟）成正比例，药物燃烧完后，y与x成反比例（如图）.现测得药物8分钟燃毕，此时室内空气中每立方米的含药量为6微克.请根据题中提供的信息，解答下列问题：

（1）药物燃烧时，y关于x的函数关系式为：

　　　　　　　　　　　　，自变量x的取值范围是：

　　　　　　　　　　　；物燃烧后，y关于x的函数关系式为：　　　　　  ；

（2）研究表明，当空气中每立方米的含药量低于1.6微克时学生方可走进教室，那么从消毒开始，至少经过　　　　　 分钟后，学生才能回到教室；

（3）研究表明，当空气中每立方米的含药量不低于3微克其持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？

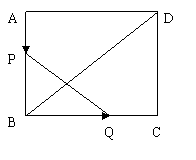27.（8分）已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点。若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？

28.（8分）如图，王华在晚上由路灯A走向路灯B，当他走到点P时，发现身后他影子的顶部刚好接触到路灯A的底部，当他向前再步行12m时到达点Q时，发现身前他影子的顶部刚好接触到路灯B的底部.已知王华的身高是1.6m，两个路灯的高度都是9.6m，且AP=QB=xm.

（1）求两个路灯之间的距离.

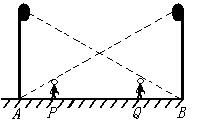（2）当王华走到路灯B时，他在路灯A下的影长是多少？