八年级数学期中调研试卷

八年级数学期中调研试卷

命题人：王明亮　　尹健兵　审核人：行者

（本试卷满分150分　　 考试时间120分钟）

亲爱的同学们，一晃我们已经度过了初二的半学期，相信在这半学期里，一定学到了不少的知识，现在是检验我们学习的时候了！下面的问题都是可以解决的，只要细心、耐心的去做，相信你一定能行！

一、　选择题（每题3分，共30分）

1.下列图案既是中心对称图形，又是轴对称图形的是（ 　 　）.

　　　　　

　  A.　　　　　　　　  B.　　　　　　　　 C.　　　　　　　　　D.

2.下列判断中正确的是（　　 ）.

A．0.25的平方根是0.5　　　　　　　B．是的一个平方根

C．的平方根是　　 　　　D．-1是1的算术平方根

3.下列各式中正确的是（　　 ）.

A.=±3　 　　 B.=－2 　　 C. =－7　D.  

4.用两个全等的三角形可以拼成的图形是（　 ）.

A.平行四边形　　 B.等腰三角形 　　C.等边三角形　　 D.等腰梯形

5.三角形中，到三个顶点距离相等的点是(　　 ) .

A．三边的垂直平分线的交点　　　　　B．三条中线的交点

C．三条角平分线的交点　　 　　　　 D．三条高线的交点

6.四边形ABCD中，O是对角线的交点，不能判断此四边形是平行四边形的是（　 ）.

A.AC=BD， AB=CD　　　　　　　　B.AD∥BC，AB∥CD，　

C.∠A=∠C，AB=CD　　　　  　　　D.AO=CO，BO=DO

7.下列能构成直角三角形三边长的是（　　）.

A. 1, 2, 3　 　　　B. 2, 3, 4 　　　　 C. 3, 4, 5　　　　 D. 4, 5, 6

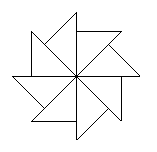
8.如图可以看作是一个等腰直角三角形旋转若干次而生成的，则每次旋转的度数可以是（　　）.

A.　　　　  B.　　　　　  C.　　　　 D.

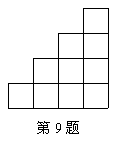
9.如图，小方格的面积是1，则图中以格点为端点且长度为5的线段有（　　 ）.

A.1条　　　　　B.2条　　 　　　 C.3条　　　　  D.4条

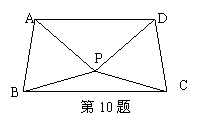
10.如图，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD，有下列四个结论： ①∠PBC=15°；②AD∥BC；③直线PC与AB垂直；④四边形ABCD是轴对称图形.其中结论正确的个数为（　　 ）.

A．1　　　　　 　　B.2　　 　　　　　C.3　 　　　　　　 D.4

	第8题

二、填空题（每题4分，共32分）

11.等腰三角形中的一个角是40°，则这个等腰三角形的底角是_____.

12.的算术平方根是　　　　　　  .

13.2005年某市完成国内生产总值（GDP）达3466.53亿元，用科学记数法保留3个有效数字是________ .

14.比较大小：　　　 .

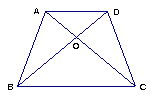
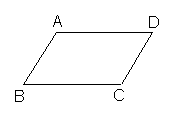15.如图，已知在四边形ABCD中，已知AB=CD，再添一个条件，使图中的四边形ABCD为平行四边形，你添的条件是　　　　　　　.

	第15题
			第16题

16.如图，在等腰梯形ABCD中，AB∥CD，对角线AC、BD交于点O，则图中全等三角形有　　　　　 对．

17.若，则　　　　　　 .

18.已知m是的整数部分，n是的小数部分， =　　　　　　 .

三、作图题（每题6分，共18分）

19.请你利用两个等腰三角形、两条线段和一个圆设计一个轴对称或中心对称图案，并附上简短的创意说明.

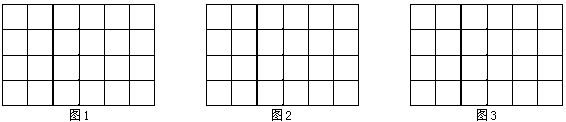
20.下图是单位长度是1的网格.

⑴在图1中画出长度为的线段AB；

⑵在图2中画出边长都是无理数的三角形ABC；

⑶在图3中画出以格点为顶点面积为5的正方形.

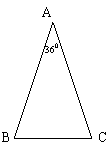
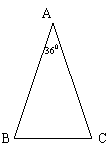
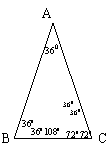
21.仿照图（a），请你再设计两种不同的分法，将△ABC分割成3个三角形，使得每个三角形都是等腰三角形. (图（b）、图(c)供画图用，作图工具不限，不要求写出画法，不要求证明；要求标出所分得的每个等腰三角形三个内角的度数) .

　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　 (a)　　　　　　　　　　　  (b) 　　　　　　　　　 (c)

四、解答题（共74分）

22.解方程：（每题4分，共8分）

（1）_；　　（2）.

 

23.已知：如图，在△ABC中，∠BAC=120⁰，以BC为边向形外作等边三角形△BCD，把△ABD绕着点D按顺时针方向旋转60⁰后得到△ECD，若AB=3，AC=2，求∠BAD的度数与AD的长（本题8分）.

24. 八年一班的小刚同学代表学校在北京参加航模比赛,这天小刚与老师, 同学兴冲冲来到机场,却遇到了一个大问题： 机场规定旅客随机携带的物品的长,宽,高不得超过1米,而小刚的飞机模型却有1.6米长,飞机模型不能折断,拆卸,托运又来不及了,怎么办呢?正当老师与同学门发愁的时候,小刚灵机一动,利用课堂上学到的知识,将飞机模型完整的带上了飞机,同样聪明的你,想到了什么办法吗?并请你将出其中的道理.（本题8分）

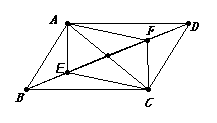
25.（1）如图1，□ABCD的对角线相交于点O，E、F分别是OB、OD的中点，四边形AECF是平行四边形吗？为什么？

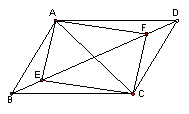
（2）如图2，□ABCD的对角线相交于点O，E、F是BD的两点，且BE=DF，上题的结论还成立吗？为什么？（本题10分）

	图1		图2

26.张老师在一次“探究性学习”课中，设计了如下数表：

	2	3	4	5	…
					…
	4	6	8	10	…
	1				…

（1）请你分别观察、、与之间的关系，并用含自然数（）的代数式表示：　　　　　  ；　　　　　　　　 ；　　　　　　　　　  ；

（2）猜想：以、、为边长的三角形是否是直角三角形？为什么？（本题10分）

27.如图所示，一根长10m的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，木棍的下端距离墙6m．若木棍上端沿墙下滑，且下端沿地面向右滑行．

（1）若木棍上端沿墙下滑1 m，请你求出木棍下端向右滑行几m？

（2）设木棍的中点为P，请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由；

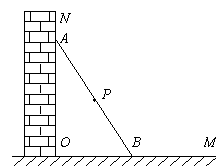（3）在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值．（本题12分）

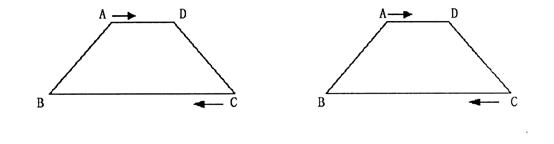
28.如图，等腰梯形ABCD中，AD∥BC，AB=CD，AD=10cm,BC=30cm，动点P从点A开始沿AD边向点以每秒1cm的速度运动，同时动点Q从点C开始沿CB边向点B以每秒3cm的速度运动，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒

（1）t为何值时，四边形ABQP是平行四边形？

（2）四边形ABQP能成为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由（本题14分）

祝贺你做完了考题，请再查一遍，看看有没有错的、漏的，别留下什么遗憾哦！