第二学期
八年级数学期中考试卷2
(考试时间:90分钟 总分120分)
班级:__________ 姓名:_________ 座号:_______ 评分:
一、选择题(每小题3分,共30分)
1.下列选项中,能写成反比例函数的是( )
A、人的体重和身高
B、正三角形的边长和面积
C、速度一定,路程和时间的关系
D、销售总价不变,销售单价与销售数量的关系
2.若分式![]() 的值为负,则
的值为负,则![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.在直角三角形中,如果一个锐角为30°,而斜边与较小直角边的和为12㎝,则斜边长为( )
A、4㎝ B、6㎝ C、8㎝ D、10㎝
4.适合下列条件的△ABC中,直角三角形有( )
①![]() ,
,![]() ,
,![]() ②
②![]() ,∠A=45° ③∠A=32°,∠B=58°
,∠A=45° ③∠A=32°,∠B=58°
④![]() ,
,![]() ,
,![]() ⑤
⑤![]() ,
,![]() ,
,![]()
A、2个 B、3个 C、4个 D、5个
5.下列各式中,正确的是( )
A、![]() B、
B、![]() C、
C、![]() (
(![]() ) D、
) D、![]()
6.若![]() ,则下列函数:①
,则下列函数:①![]() ②
②![]() ③
③![]()
![]()
![]() )
)
④![]() ,其中
,其中![]() 随
随![]() 的增大而增大的是( )
的增大而增大的是( )
A、① ② B、② ③ C、③ ④ D、① ③
7.若![]() ,则
,则![]() 可用含
可用含![]() 的式子表示为( )
的式子表示为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8.在同一坐标系中,函数![]() ,
,![]() (
(![]() )的图象是( )
)的图象是( )
A、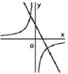 B、
B、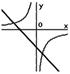 C、
C、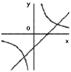 D、
D、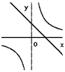
9.若M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),P(
),P(![]() ,
,![]() )三点都在函数
)三点都在函数![]() (
(![]() )的图象上,则
)的图象上,则![]() 、
、![]() 、
、![]() 的大小关系为( )
的大小关系为( )
A、![]() >
>![]() >
>![]() B、
B、![]() >
>![]() >
>![]() C、
C、![]() >
>![]() >
>![]() D、
D、![]() >
>![]() >
>![]()
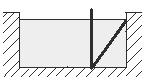 10.小刚准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5米远的水底,竹竿高出水面0.5米,保持底端不动,把竹竿的顶端拉到岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
10.小刚准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5米远的水底,竹竿高出水面0.5米,保持底端不动,把竹竿的顶端拉到岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A、2米 B、2.5米 C、2.25米 D、3米
二、填空题(每小题3分,共24分)
11.用科学记数法表示![]() 的运算结果为____________。
的运算结果为____________。
12.若函数![]() 是反比例函数,则
是反比例函数,则![]() =__________。
=__________。
 13.计算:
13.计算:![]() =__________。
=__________。
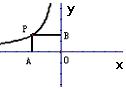
14.如图:P是反比例函数![]() 的图象上的点,过点P作
的图象上的点,过点P作![]() 轴、
轴、
![]() 轴的垂线,垂足分别为A、B,且四边形PAOB的面积为4,
轴的垂线,垂足分别为A、B,且四边形PAOB的面积为4,
 则
则![]() 与
与![]() 的函数关系式是____________。
的函数关系式是____________。
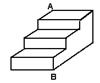
15.如图是一个三级台阶,它的每一级的长、宽和高分别为
20分米、3分米、2分米,A和B是这个台阶两个端点,
A点有一只蚂蚁想到B点去吃可口的食物,则蚂蚁沿着
台阶面爬到B点的最短路线是______分米。
 16.一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后,相距_______千米。
16.一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后,相距_______千米。
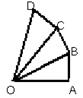
17.如图,∠OAB=∠OBC=∠OCD=90°,AB=BC=CD=1,
OA=2,则OD=_______。
18.已知一直角三角形的三边为![]() ,其中斜边长
,其中斜边长![]() 为13,
为13,
并且周长为30则这个直角三角形斜边上的高为_________。
三、解答题(前4小题各5分,后2小题各6分,共32分)
19.计算:(1)![]()
(2)![]()
(3)![]()
20.先化简,再请你把你喜欢的数代入求值
![]()
21.(6分)解方程:![]()
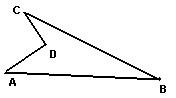
22.(6分)如图的一块地,∠ADC=90°,AD=8m,CD=6m,AB=26m,BC=24m,求这块地的面积
 |
四、实际应用题(每小题6分,共12分)
23.(2005年青岛中考题)为响应承办“绿色奥运”的号召,某中学初三(1)
班计划组织部分同学义务植树180棵,由于同学们参与的积极性很高,实
际参加植树活动的人数比原计划增加了50%,结果每人比原计划少栽了2
棵树,问实际有多少人参加了这次植树活动?
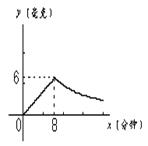 24.为了预防“非典”,某单位对办公室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量
24.为了预防“非典”,某单位对办公室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (分钟)成正比例,药物燃烧后,
(分钟)成正比例,药物燃烧后, ![]() 与
与![]() 成反比例(如图),观察得知药物8分钟燃尽,此时室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
成反比例(如图),观察得知药物8分钟燃尽,此时室内空气中每立方米的含药量为6毫克,请你根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,![]() 关于
关于![]() 的函数关系式是___________,
的函数关系式是___________,
自变量![]() 的取值范围是____________;
的取值范围是____________;
(2)药物燃烧后,![]() 关于
关于![]() 的函数关系式是___________,
的函数关系式是___________,
自变量![]() 的取值范围是____________;
的取值范围是____________;
(3)研究表明,当空气中每立方米的含药量不高于1.6毫克
时方可入室,那么从消毒开始,至少需要经过_________分钟方可入室。
五、推断题(6分)
25.将![]() 代入函数
代入函数![]() 中,所得函数值记为
中,所得函数值记为![]() ,又将
,又将![]() 代入函数
代入函数![]() 中,所得的函数值记为
中,所得的函数值记为![]() ,再将
,再将![]() 代入函数中,所得函数值记为
代入函数中,所得函数值记为![]() …,继续下去。
…,继续下去。
![]() =________;
=________;![]() =________;
=________;![]() =_________;
=_________;![]() =_________。
=_________。
六、证明题(8分)
28.已知:如图,△ABC中,AB>AC,AD为BC边上的高,
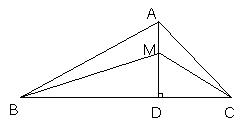 M是AD边上任意一点
M是AD边上任意一点
求证:![]()
七、综合题(8分)
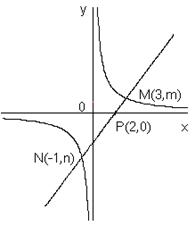 29.如图,一次函数
29.如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于M、N两点,与
的图象交于M、N两点,与![]() 轴分别交于点P(2,0),且PN=5。
轴分别交于点P(2,0),且PN=5。
(1)求反比例函数和一次函数的关系式;
(2)求△OMN的面积;
(3)根据图象写出使反比例函数的值大于
一次函数的值的![]() 的取值范围。(不要求
的取值范围。(不要求
写出过程)
附加题(分数不加在总分中)
1、(10分)金星笔厂生产一批成本为2元的自动笔,在市场营销中发现,此种笔的日销售单价![]() (元)与日销售量
(元)与日销售量![]() (枝)之间有如下关系:
(枝)之间有如下关系:
|
| 3 | 4 | 5 | 6 |
|
| 20 | 15 | 12 | 10 |
(1)猜测并确定![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设经营此种自动笔的销售利润为P元,试求出P与![]() 之间的函数关系式,若物价局规定此笔的销售价最高不能超过10元/枝,请你求出当日销售单价
之间的函数关系式,若物价局规定此笔的销售价最高不能超过10元/枝,请你求出当日销售单价![]() 定为多少时,才能获得最大日销售利润?
定为多少时,才能获得最大日销售利润?
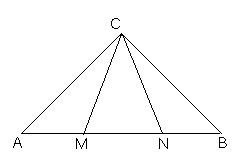 2、(10分)在等腰三角形Rt△ABC中,∠ACB=90°,AC=BC,M、N在斜边上,且∠MCN=45°
2、(10分)在等腰三角形Rt△ABC中,∠ACB=90°,AC=BC,M、N在斜边上,且∠MCN=45°
求证:![]()