八年级数学期中试题1
班别： 学号： 姓名： 得分：
一、选择题
1. 下列各组数分别为一个三角形三边的长，其中能构成直角三角形的一组是（ ）
A. 3,4,5 B. 7,12,15 C. 13,16,20 D. 8,24,25
2. 下列说法正确的是（ ）
A. 无理数包括正无理数和负无理数 B. 实数只包括有理数和无理数
C. 无理数就是无限小数 D. 不带根号的数都是有理数
3. 下列图形，既是轴对称图形又是中心对称图形的是（ ）
A. 菱形、正方形、圆 B. 平行四边形、菱形、正方形
C. 等腰梯形、矩形、正方形 D. 正三角形、矩形、圆
4. 下列性质中，菱形具有而矩形不具有的是（ ）
A. 内角和等于3600 B. 对角线平分一组对角
C. 对角相等 D. 邻角互补
5. 用形状大小完全相同的下列图形不能进行密铺的是（ ）
A. 正六边形 B. 正多边形 C. 平行四边形 D. 等腰三角形
6. 下列命题：①平行四边形的对角线互相平分 ②对角线互相平分的四边形是平行四边形③正方形的对角线互相垂直 ④对角线互相垂直的四边形是正方形，其中正确的有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
7. 下列各式中，正确的是（ ）
A. 
B. ±
C. 
D. 
8. 在图形的旋转中，下列说法中错误的是（ ）
A. 图形上的每一点移动的角度相同 B.图形上任意两点的边线与其对两点的边线相等
C. 图形上的每一点旋转中心的距离相等 D. 图形上可能存在不动点
9.点P（－4,1）在平面直角坐标系中所在的象限是（ ）
A. 四 B. 三 C. 二 D. 一
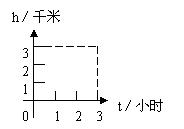
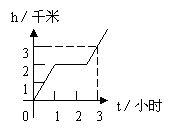10. 某游客为爬上3千米高的山顶看日出，先用1小时爬上了2.4千米，休息了1小时后，再用1小时爬上山顶，游客爬山所用时间t（小时）与山高h(千米)间的函数关系用图表（ ）
 |
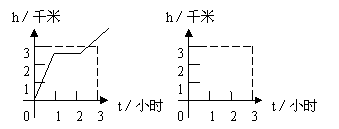A B C D
二、填空题
1. 4的平方根是 ，8的立方根是 ，
的算术平方根是 。
2. 直角三角形的一条直角边长为3cm，斜边长为5cm，则斜边上的高为 。
3. 五边形的内角和是 ，十边形外角和是 。
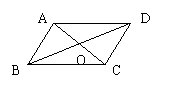
4. 如图在四边形ABCD中，对角线AC与BD相交于
点O，当满足条件 时，
它为平行四边形。（填写一个你认为正确的一个条件即可）
5. 若一条直线在
，当X＝1时，y＝2；当x＝0时y＝3，则直线的表达式为 。
6. 对于函数
，y随x的 而减小。
7. 点A（3,2）关于X轴对称点B的坐标为 。
8. 菱形的周长为40cm，一对角线长是12cm,那么这个菱形的面积为 。
9. 已知矩形两条对角线的一个交角为600，矩形的短边长为4cm，则它的对角线长 cm,长边为 cm。
10. 如图，已知线段AB绕O点旋转后，点A的对应点为C，请画出旋转后的线段。
 |
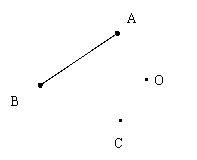三、计算
1.
2. 
四、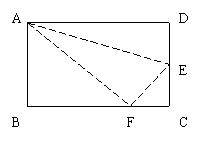
如图所示折叠长方形的一边AD，点D落在BC边的点F处，已知AB＝8cm，BC＝10cm,求EC的长。
五、如图，四边形ABCD是矩形，对角线AC、BD相交于O，CE∥DB，交AB的延长线E，度证明AC＝CE。
六、如图，已知△ABC中，AD平分∠BAC，DE∥AC，DF∥AB。
⑴试证明四边形AEDF的形状。
⑵当△ABC满足什么条件时，四边形AEDF为正方形，为什么？
七、某食品厂向A市销售饼干，如果从铁路托运每千克需运费0.58元，若从公路运送每千克需运费0.28元，另需出差补助费600元。
⑴高该厂向A市销售饼干X千克，从铁路需运费y1元，从公路需运费y2元，分别写出两种运送方案所需费用y与x之间的关系式。
⑵当向A市销售饼干多少千克时，两种运送方案所需费用一样多？
⑶设销售的饼干重量为2500千克，讨论哪种运送方案更合算？
八、已知A地在B地正南方向3km处，甲、乙两地向正方向匀速直行，他们与A地的距离S（km）所行时间t(h)之间的关系如图所示，其中l1表示甲运动的过程，l2表示乙运动的过程，根据图象回答：
（1） 甲和乙哪一个在A地，哪一个在B地？
（2） 甲用多长时间追上了乙？
（3） 求出l1，l2的函数表达式？
（4） 通过计算说明何时两人又相距3km？