八年级数学调研试卷
（第一部分选择与填空）
一、选择题（每题4分，共48分）
1．下列图案中，不是是轴对称的图案是
A． B． C． D．
2．下列图形中不一定是轴对称图形的是
A．角 B．线段 C．直角三角形 D．等腰三角形
3．在下列四组线段中，能组成直角三角形的是
A．a=2，b=3，c=4 B．a=1，b=2，c=3
C．a=3,b=4,c=5 D．a=7，b=8，c=9
4．等腰三角形一边长是4，另一边长是9，则它的周长是
A．17 B．22 C．17或22 D．24
5．等腰三角形一个角等于70o，则它的底角是
A．70o B．55o C． 60o D． 70o或55o
6．下列说法：①成轴对称的两个图形全等；②两个图形全等一定成轴对称；③成轴对称的两个图形的对称轴是对称点连线的垂直平分线；④等腰梯形的对称轴是过两腰中点的一条直线。以上结论正确的个数为
A．1个 B．2个 C．3个 D．4个
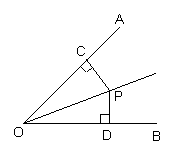
7．如图，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则PC与PD的大小关系 A．PC＞PD B．PC＝PD C．PC＜PD D．不能确定
8． 如图，在△ABC中，BC = 8 cm，AB的垂直平分线交AB
于点Ｄ，交边AC于点E，△BCE的周长等于18 cm，则
AC的长等于
A．6 cm B．8 cm
C．10 cm D．12 cm
9．直角三角形的两直角边长为5、12，则其斜边上的高为
A．6 B．8 C．
D．
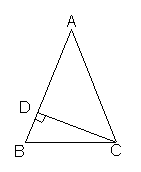
10．如图，等腰三角形ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于
A、44° B、68° C、46° D、22°
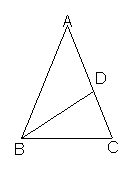
11．如图，在△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为
A．70°
B．45° C．36°
D．30°
|
|
12．观察下列图形并填表：
| 梯形个数 | １ | ２ | ３ | ４ | … | ｎ |
| 周 长 | ５ | ８ | 11 | 14 | … |
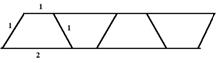
表中应填
Ａ．3n＋1 Ｂ.2n＋1 Ｃ. 3n＋2 Ｄ.2n＋2
二、填空题（13～16每题4分，17题每空4分，共有28分）
13．等边三角形有 条对称轴，长方形有 条对称轴
14．在我们学过的汉字中有很多是轴对称图形，请你认真地写出两个
15．一个直角三角形的两条直角边长为6，8，则该直角三角形斜边上的中线的长度为
16．如图，图中的字母S所代表的正方形的面积为
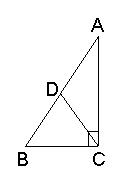
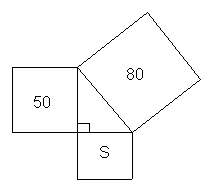17．如图，AC⊥BC，AD=BD，图中相等的角有：
，等腰三角形有：
；如果再增加一个条件：
，图中的△BCD就是等边三角形.
 |
|
八年级数学调研试卷 2005、10
（第二部分 答卷纸）
（测试内容：1.1～2.1, 分值150分， 考试时间100分钟）
| 题 号 | 一 | 二 | 三 | 总分 | |||
| 18 | 19 | 20 | 21 | ||||
| 得 分 | |||||||
一、选择题（每题4分，共48分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（13～16每题4分，17题每空4分，共28分）
13． ， 14． 15．
16． ，17． ， ，
三、解答题（共74分）
18．说理题（10+11+12=33分）
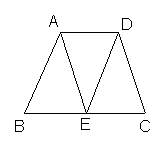(1)如图，梯形ABCD中，AD∥BC，AB=CD，点E是BC的中点，试说明AE=DE
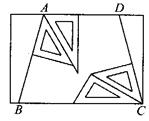
(2)在长方形纸上按如图所示的画法，所得梯形是不是等腰梯形？为什么？
 |
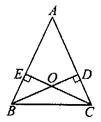(3)如图，△ABC的2条高BD、CE相交于点O，且OB=OC，AB与AC相等吗？为什么？
19．作图题（9+10=19分）
(1)为了缓解A、B、C三个村庄灌溉用水问题，决定建一个水电站D，满足这个水电站到三个村庄的距离相等，请你用圆规和尺找出点D的位置（保留作图痕迹，不写作法）
(2)如图，点A、B、C 3点都在方格纸的格点位置上，请你再找出格点D，使图中的4点组成一个轴对称图形。
 |
20．推理与计算（本题满分14分）
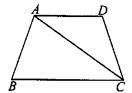
（A类10分）如图，在梯形ABCD中，AD//BC，AB=DC=AD，AC=BC，求∠B的度数。
（B类14分）如图，在△ABC中，∠BAC=90°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA。
(1) 试求∠DAE的度数。
(2) 如果把第（1）题中“AB=AC”的条件去掉，其余条件不变，那么
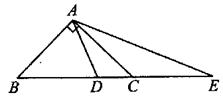∠DAE的度数会改变吗？
|
你选择的是 类
解答过程如下：
21．（操作与设计，本题满分8分）
以给定的图形“
、△、△、=（两个圆、两个三角形、两条平行线）”为构件，设计一个独特且有意义的轴对称图形。举例：如图所示的左框中是符合要求的一个图形，你还能构思出其它图形吗？请在右框中画出与之不同的一个图形，并写出一两句贴切、诙谐的解说词。
 |
。