八年级数学（下）第17章复习
一、选择题（每小题2分，共20分）
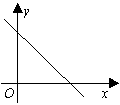1. 已知直线y=kx+b如图所示，要使y的值为正，自变量x必须满足（ ）.
（A）x＜0 (B)x＞0
(C)x＜
(D)x＞
2. 已知一次函数y=-x+3,当0≤x≤3时，函数y的最大值是( ).
A.0 B.3 C.-3 D.无法确定
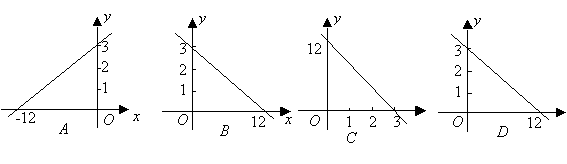3. 李红同学带了3元钱买本子，若每本0.25元，则他买本子数x与所剩人民币y（元）的关系是下图中的（
）
4. 在同一坐标内，函数关系式为y=kx+b(k、b为常数且k≠0)的直线有无数条，在这些直线中，不论怎样抽取，至少要抽几条直线，才能保证其中的两条直线经过完全相同的象限（ ）.
（A）4 （B）5 （C）6 （D）7
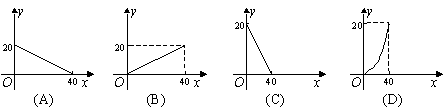
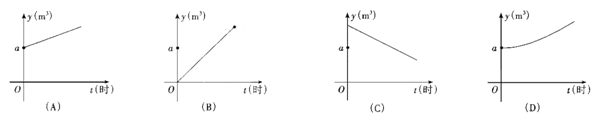5. 如图，一水库现蓄水a立方米，从开闸放水起，每小时放水b立方米，同时从上游每小时流入水库2b立方米，那么到水库蓄满水为止，水库蓄水量y（立方米）是开闸时间t（时）的函数，其图象只能是图中的（ ）.
6. 如图，如果函数y=k(x-1)和函数y=
（其中k是不等于零的常数）的图象在同一直角坐标系中，则其图象应为（ ）.
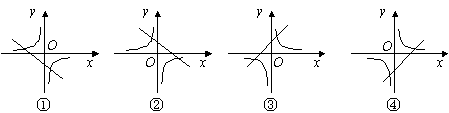
（A）①或③ （B）②或③ （C）②或④ （D）①或④
7. 一根蜡烛点燃2分钟长为19厘米，点燃12分钟时长为14厘米，那么蜡烛剩余长度y（厘米）与点燃时间x（分）的关系是（ ）.
8. 如图是温度计的示意图，左边的温度表示摄氏温度，右边的温度表示华氏温度，则华氏温度y(℉)与摄氏温度x (℃)之间的函数关系式为（ ）
A.
B. 
C. 
D. 
9. 一次函数
的图象经过点（2，-1）和（0，3）.那么这个一次函数的表达式为（ ）
A．
B. 
C. 
D. 
10. 某乡的粮食总产量为a（a为常数）吨,设该乡平均每人占有粮食为y（吨），人口数为x，则y与x之间的函数关系的图象应为（ ）.
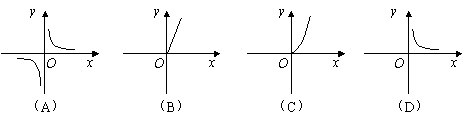
二、填空题（每小题2分，共20分）
1. 直线y=x-3与直线y=4x+1的交点为 .
2. 下列函数中为一次函数的是:_________（写出序号）
(1)
(2) 
(3) 
(4) 
(5) 
(6) 
3. 若反比例函数y=的图象在第二、四象限，则直线y=kx+4不经过第 象限.
4. 已知直线y=ax+b上两点（x1,y1）和(x2,y2),且a+b＜0,ab＞0,当x1＞x2时，y1与y2的大小关系式为 .
5. 圆心都在y轴上的两圆相交于A、B两点，如果A点的坐标为（2，
），那么B点的坐标为 .
6. 若一次函数y=-x+a与一次函数y=x+b的图象的交点坐标为（m,8）.则a+b=______.
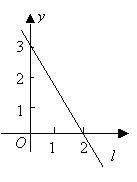7. 如图，直线l是一次函数y=kx+b的图象，看图填空：
(1) b=______,k=______;
(2) x=-20时,y=_______;
(3) 当y=-20时,x=_______.
8. 若一次函数y=kx+b交于y轴的负半轴，且y的值随x的增大而减小，则k_____0,b______0.(填">"、"="、或"<")
9. 点P(x,y)满足xy=0, 点P一定在 上.
10. 若y与z成正比例，x与z成反比例，则y与x成 .
三、解答题（每小题5分，共50分）
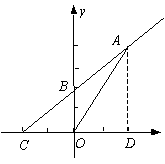1. 如图，一次函数y=kx+b的图象经过A(2,4)和B(0,2)两点，
且与x轴相交于C点.
（1） 求这个一次函数的表达式；（2）求△AOC的面积.
2. 已知△ABC的顶点B（0，0），C（3，4），顶点A在y 轴上，S△ABC=3，求点A的坐标及直线AC的解析式.
3. 十堰市广电局与长江证券公司联合推出广电宽带网业务，用户通过宽带网可以享受新闻点播、点击武当、影视欣赏、股市大户室等服务.其上网费用方式有三种.
方式一：每月80元包干；
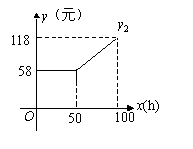
方式二：每月上网时间x(h)与上网费y（元）的函数关系
如图中的折线段所示；
方式三：以0小时为起点，每小时收费1.6元，月收费
不超过120元.
若一用户上网x(h)，月上网总费用为y元.
（1）根据图,写出方式二中y与x的函数关系式(0≤x≤100)
(2)试写出方式三中，y与x的函数关系式(0≤x≤75)
(3)试问此用户每月上网60h,选用哪种方式上网，其费用最小？
4. 分别写出下列问题中的函数关系式，并指出自变量的取值范围.
（1） 50千米的路程，以v（千米/时）的速度前进，所用的时间为t（时），t与v之间的函数关系式；
（2） 半径为2的圆柱体的体积为V(m3),高为h（米）,V与h的函数关系式；
（3） 一栋住宅楼，底层高4m，以上每层高3m，楼高H与层数n之间的函数关系式；
（4） 1吨民用自来水的价格为2.35元，所交水费y(元)与使用自来水的数量n（吨）的函数关系式.
5. 小华感冒发烧，临睡前吃了热镇痛药，妈妈每隔两小时给她测一次体温，测得结果如下表：
| 时刻 | 18 | 20 | 24 | 2 | 4 | 6 | 8 | 10 | 12 |
| 体温（℃） | 38.4 | 38.5 | 38.1 | 37.6 | 37.2 | 36.9 | 36.7 | 36.3 | 36.2 |
看表回答小华什么时候体温最高，什么时间体温最低，利用周日休息时间每隔两小时测一下自己的体温，并填写出表格.
6. 已知y+m与x-n成正比例（其中m,n为常数），请说明：y是x的一次函数.
7. 已知一次函数y=(4m+1)x-(m+1)
(1) m为何值时，y随x的增大而减小？
（2）m为何值时，直线与y轴的交点在x轴的下方？
（3）m为何值时，直线位于第二、三、四象限？
8. 某校组织学生到距离学校6千米的光明科技馆去参观，小王因事没能乘上学校包车，于是准备在学校门口改乘出租车去光明科技馆.出租车的收费标准如下：
（1） 写出出租车行驶的里程数
（千米）与费用y（元）之间的函数关系式.
（2） 小王身上有11元钱，求出租车到科技馆的车费够不够？请说明理由.
答案
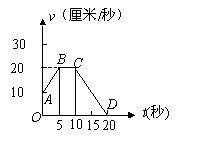
9. 右图所示为质点在20秒内运动的速度-时间图象，写出速度-时间函数.
10. 一个菱形的两条对角线长分别是6和4
，取两条对角线所在的直线为坐标轴，求四个顶点的坐标.
四、解答题（每小题5分，共10分）
1. 某家电集团公司生产某种型号的新家电.前期投资200万元，每生产1台这种新家电，后期还需要其他投资0.3万元，已知每台新家电可实现产值0.5万元.
(1)求总投资额y1（万元）和总利润y2（万元）关于新家电的总产量x（台）的函数关系式；
(2)当新家电的总产量为900台时，该公司的盈亏情况如何？
(3)请你利用第（1）小题中y2与x的函数关系式，分析该公司的盈亏情况.（注：总投资=前期投资＋后期其他投资，总利润=总产值－总投资）.
2. 某博物馆每周都吸引大量中外游客前来参观.如果游客过多，对馆中的珍贵文物会产生不利影响，但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入，因此，博物馆采取了涨浮门票价之间存在着如图所示的一次函数关系，在这样的情况下，如果要确保每周4万元的门票收入，那么每周应限定参观人数是多少？门票的价格应是多少元？