八年级数学第二次统测试卷
班别： 学号： 姓名： 成绩：
一、填空题（每小题3分 共42分）
1．计算：
。
2．如图，已知
，要使⊿
≌⊿
，
只需增加的一个条件是 。
3．分解因式：
4．函数关系式
中的自变量
的取值范围是 。
5．等腰三角形的一个角是
，则它的另外两个角的度数是
。
6．一次函数
的图象经过 象限。
7. 对直线y=3x-15，当x____________时，y<0;
8.若
是一个完全平方式，则
=
。
9. 如图，在⊿ABC中,∠BAC=60°，将 ⊿ ABC绕着点A顺时针旋转40°后得到 ⊿ADE,
则∠BAE=__________.
10. 已知点M的坐标为(3,2)它关于x轴的对称点是N,点N的坐标是__________.
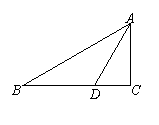
11. 如图，在△ABC中，∠C=90°，AD平分∠BAC，BC=10cm，BD=7cm，则点D到AB的距离为_____________cm．
9题 
11题
12题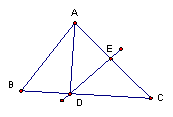
12. 如图，⊿ABC中，DE是AC的垂直平分线，AE=3cm.⊿ABD的周长是13cm，则⊿ABC的周长为__________.
13已知在一个样本中，50个数据分别落在5个组内，第一、二、三、四、五组数据的个数分别是2、8、15、20、5，则第四组的频率为 。
14、若
与
是同类项，则
=
。
二、选择题（每题3分 共30分）
1、下列计算中，正确的是（ ）
（A）
;（B）
; C、
; D、
2、下面有4个汽车标致图案，其中是轴对称图形的是 ( )
① ② ③ ④
A、②③④ B、①②③ C、①②④ D、①②④
3、如图,两条直线
和
的交点坐标可以看作下列方程组中（ ）的解．
A、
B、
C、
D、
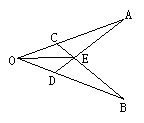
4、如图，已知OA=OB，OC=OD，AD，BC相交于E，则图中全等三角形的个数是（ ）．
A、5 B、4 C、3 D、2
 |
 |  |  | |||
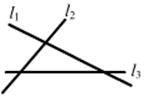
5、如图，l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有（ ）
A、四处 B、三处 C、二处 D、一处
6．已知一次函数y=kx+b的图象（如图），当y＜0时，x的取值范围是（ ）
（A）x＞0 （B）x＜0 （C）x＜1 （D）x＞1
7．如图是某蓄水池的横断面示意图，分为深水池和浅水池，如果这个蓄水池以固定的注水，下面能大致表示水的最大深度h与时间t之间的关系的图像是( )
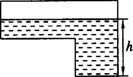
8．若
是完全平方式，则
的值是（ ）
A、4 B、8 C、
4 D、8
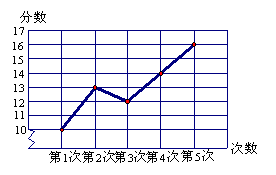
9．小明同学参加某体育项目训练，近期的五次测试成绩得分情况如右图所示：则小明同学五次成绩的平均分是（ ）
（A）12分（B）13分（C）14分（D）15分
10.下列各式从左到右的变形中，是因式分解的为（ ）
A、
B、
C、
D、
三、解答题（共48分）
1.计算题：
(6分) 2.分解因式: -
(6分)
3．（8分）先化简，再求值：
，其中
.
4.已知一次函数图象经过（3，5）和（—4，—9）两点，①求此一次函数解析式；(6分)
②若点（a，2）在函数图象上，求a的值。(3分)
5、已知：如图，D是△ABC的边AB上一点，AB∥FC，DF交AC于点E，DE＝EF。
 |
求证：AE＝CE。(7分)
6.某移动通讯公司开设两种业务：
| 业务类别 | 月租费 | 市内通话费 | 说明：1分钟为1跳次，不足1分钟按 1跳次计算，如3.2分钟为4跳次． |
| 全球通 | 50元 | 0.4元/跳次 | |
| 神州行 | 0元 | 0.6元/跳次 |
若设某人一个月内市内通话x跳次，两种方式的费用分别为y元和y元．
问: ①写出y、y与x之间的函数关系式；(4分)
②一个月内市内通话多少跳次时，两种方式的费用相同？(4分)
③某人估计一个月内通话300跳次，应选择哪种方式合算？(4分)