八年级数学第二学期教学质量自查
(满分100分)
一、选择题（每小题3分，共15分）
1、下列计算正确的是（ ）
A.
B.
C.
D.
2、函数
的图象过点（1，-2），则此函数的图象在平面直角坐标系中的（ ）
A.第一、三象限 B.第三、四象限
C.第一、二象限 D.第二、四象限
3、若
ABC
A`B`C`,∠A=40°,∠B=110°,则∠C`等于（ ）
A．40° B.110° C.70° D.30°
4、某班的男女生人数之比是3:2,制作扇形统计图时女生对应的扇形的圆心角是( )
A.144° B.216° C.72° D.108°
5、在直角三角形中,若一个锐角为30°,斜边与较小直角边的和为18cm，则较大直角边为（ ）cm.
A.4 B.6 C.3
D.6
二、填空题（每小题3分，共15分）
6、矩形的长a=
㎝，宽b=
㎝，则这个矩形的面积为
㎝2.
图1
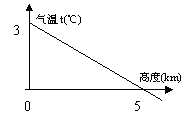
7、如图1，是某地气温t(℃)随着高度h（千米）的升高而降低的关系图，观察图象可知该地地面气温是 ℃
8、如果两个相似三角形对应高的比是1：2，那么它们的面积比是 。
9、已知A、B两点，如果A对B的俯角为35°，那么B对A的仰角为 。
10、对甲、乙两台机床生产的零件进行抽样测量，其平均数、方差计算结果如下：机床甲：x甲=10，S2甲=0.20;机床乙：x乙=10，S2乙=0.06,由此可知：
机床性能好。
三、解答题（每小题6分，共30分）
11、计算：5
-4
12、已知函数y1=x-6和y2=2x+3.
(1)在所给的坐标系中画出这两个函数的图象；
(2)写出这两个函数图象的交点坐标。
13、如图2，一架长2.5m的梯子，斜靠在一竖直的墙上，这时，梯底距墙底端0.7m，如果梯子的顶端沿墙下滑0.4m,则梯子的底端将滑出多少米？
 |
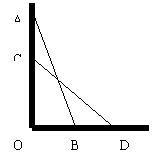图2
14、将下列事件发生的机会从小到大在直线上排序：
（1）掷一枚普通的正六面体的骰子点数是8；
（2）在1-100中产生一个随机整数恰好是偶数；
（3）抛两枚普通硬币恰好出现两个反面；
（4）从装有2个红球和3个黄球的袋子中摸出一个恰好不是黑球。
15、如图3， 
～
，AE=5，EC=3，BC=7。
求：（1）DE的长；
（2）DE与BC平行吗？试说明理由。
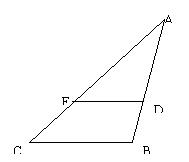
图3
四、解答题：（每小题8分，共40分）
16、计算： 
×
+
÷
| 上海 | 杭州 | 合肥 | 南京 | 无锡 | 扬州 | 徐州 | 苏州 | 桂林 | 西安 | |
| 最高气温 | 2 | 2 | 3 | 2 | 1 | 2 | 3 | 1 | 3 | 1 |
| 最低气温 | 0 | -2 | -3 | -3 | -2 | -4 | -7 | -6 | 2 | 5 |
17、下表列出的是2006年1月6日6时发布的城市天气预报中部分城市的最高气温和最低气温（单位：℃）：
（1） 这些城市最高气温的极差是多少？最低气温的极差是多少？
（2） 这些城市最低气温的标准差是多少？（结果保留4个有效数字）
18、如图4，为了测量一条河的宽度，一测量员在河岸边的C处测得对岸一棵树A在正南方向，测量员向正东方向走180米到点B处，测得这棵树在南偏西59°的方向，求河的宽度（结果保留4个有效数字）。
 |
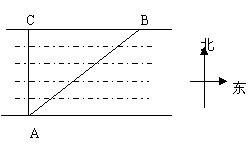图4
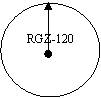19、某衡器厂的RGZ-120型体重秤，最大称量120千克，你在体检时可看到如图5显示盘，已知，指针顺时针旋转角x(度)与体重y(千克)有如下关系：
| X(度) | 0 | 72 | 144 | 216 |
| Y(千克) | 0 | 25 | 50 | 75 |
（1） 根据表格的数据在平面直角坐标系中描出相应的点，顺次连结各点后，你发现这些在哪一种函数的图象上？ 图5
（2） 求出函数解析式并写自变量x的取值范围；
（3） 当指针旋转到158.4度的位置时，显示盘上的体重读数模糊不清，请你求出此时的体重。
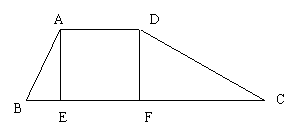
20、为防水患，在东江上游修筑了防洪堤，其横截面为一梯形（如图6所示），堤的上底宽AD和堤高都是`6米，其中
。
（1）求证：
～；
（2）如果
，求堤的下底BC的长。
图6