八年级数学第二学期期末测试卷
学校______班级_______姓名______得分_________
一、选择题（本大题10个小题，每小题4分，共40分）
1、一件工作，甲独做a小时完成，乙独做b小时完成，则甲、乙两人合作完成需要( )小时。
A、
B、
C、
D、
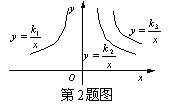
2、如图是三个反比例函数
，
，
在x轴上方的图象，由此观察得到
、
、
的大小关系为（ ）
A
B 
C 
D
|
3、如图，点A是反比例函数
图象上一点，AB⊥y轴于点B，则△AOB的面积是（ ）
A、1 B、2 C、8 D、4
4、三角形三边长分别为2n2+2n， 2n+1， 2n2+2n+1（n为正整数）这样的三角形是（ ）
A、锐角三角形 B、直角三角形
C、钝角三角形 D、钝角三角形 或直角三角形
5、若反比例函数y=
经过（ －1，2 ），则一次函数y=－kx + 2的图象一定不经过
（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
6、如图1，在梯形ABCD中，AD∥BC，AB=DC，∠C=60°，BD平分∠ABC．如果这个梯形的周长为30，则AB的长为（ ）．
（A）4 （B）5 （C）6 （D）7
7、已知：在Rt△ABC中，∠ACB=90º，周长为24，M是AB的中点且MC = 5，则△ABC的面积为（ ）
A、30 B、24 C、48 D、12
8、当5个整数从小到大排列，则中位数是4，如果这5个数的唯一众数是6，则这5个整数可能的最大和是（ ）
A、21 B、22 C、23 D、24
9、如图，在一个由4×4个小正方形组成的正方形网格中，
阴影部分面积与正方形ABCD的面积比是（ ）
A、3：4 B、5：8 C、9：16 D、3：8
10、已知四边形ABCD的对角线相交于O，给出下列 5个条件①AB∥CD ②AD∥BC③AB=CD ④∠BAD=∠DCB，从以上4个条件中任选 2个条件为一组，能推出四边形ABCD为平行四边形的有（ ）
A6组 B.5组 C.4组 D.3组
二、填空题（每小题4分，共40分）
11、顺次连结四边形的中点所得的四边形是______顺次连结平行四边形四边的中点所得的四边形是______顺次连结矩形四边的中点所得的四边形是______顺次连结菱形四边的中点所得的四边形是_______。
12、已知（x1,y1),(x2 ,y2 )是反比例函数图象上的两点，当x1>x2>0时，y1<y2，则K的取值范围是___________
 |
14、直角三角形两直角边的长分别为5和12，则斜边上的高为____________
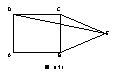
15、以边长5cm，4cm，7cm的三条线段中的两条为边，另一条为 对角线画平行四边形，可以画出形状不同的平行四边形的个数__________
16、如图在正方形ABCD外，以BC为边作等边三角形BCE，则∠DEC=________
17、数据1，2，8，5，3，9，5，4，5，4的众数是_________；中位数是__________。
18、甲乙两人做某种机器零件，已知甲每小时比乙多做6个，甲做90个用的时间与乙做60个所用的时间相等，设乙每小时做x个根据题意可列出的方程为 。
19、已知，在△ABC中,AB＝1,AC＝
,∠B=45°,那么△ABC的面积是
。
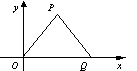
20、如右图，△OPQ是边长为2的等边三角形，若反比例函数的图象过点P，则它的解析式是_______。
三、解答题（共70分）
21、（1）（7分）先化简再求值 
。其中x=
. y=
（2）（5分）
22（5分）已知函数y = y1－y2，y1与x成反比例，y2与x－2成正比例，且当x = 1时，y =－1；当x = 3时，y = 5.求当x＝5时y的值。
23（5分）如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形。
（1）使三角形三边长为3，，
。
（2）使平行四边形有一锐角为45°，且面积为4
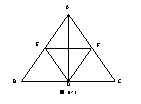
24．（8分）如图：在△ABC中， AD⊥BC 于D， E、F、分别是AB、AC边的中点，连结DE、EF、FD，当△ABC满足什么条件时，四边形AEDF是菱形 ，并证明。
25、（12分）如图，等腰梯形
中，
．
、
分别是
、
的中点，
、
分别是
、
的中点．(1) 证明：四边形
是菱形；
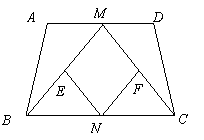(2) 若四边形是正方形，请探索等腰梯形的高和底边的数量关系
26、（5分）某校师生到距学校20千米的公路旁植树，甲班师生骑自行车先走，45分钟后，乙班师生乘汽车出发，结果两班师生同时到达，已知汽车的速度是自行车速度的2.5倍，求两种车的速度各是多少?
27、(10分)张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”，对两位同学进行了辅导，并在辅导期间进行了10次测验，两位同学测验成绩记录如下表：
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 | |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | 80 |
利用表中提供的数据，解答下列问题：
（1）填写完成下表：
（2）张老师从测验成绩记录表中，求得王军10次测验成绩的方差
=33.2，请你帮助张老师计算张成10次测验成绩的方差
；（3）请你根据上面的信息，运用所学的统计知识，帮助张老师做出选择并简要说明理由。
28、（12分）如图所示，一根长2a的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，设木棍的中点为P。若木棍A端沿墙下滑，且B端沿地面向右滑行。
（1）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由。
（2）在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值。