八年级数学第二学期期末检测试题卷
检测范围：浙教版《数学》八年级（下）全册
第一试（满分100分）
一、选择题(每题3分,共30分)
1、要使二次根式
有意义，字母x必须满足的条件是（ ）
A. 
B. 
C. 
D. 
2、方程
的根是 （ ）
A. x=0 B. x=1 C. x1=0，x2=1 D. 无实数根
3、在平行四边形ABCD中,∠A=115°，则∠C的度数是（ ）
A．105° B. 115° C.125° D.65°
4、八年级某班50位同学中，1月份出生的频率是0.20，那么这个班1月份生日的同学有（ ）
A. 10位 B. 11位 C. 12位 D. 13位
5、下列各数中,可以用来证明命题“对于任何自然数n,代数式
的值都是负数”是假命题的反例是( )
A.n=3 B. n=5 C. n=6 D. n=8
6、下列图形中，既是轴对称图形，又是中心对称图形的是 ( )
 | |||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
7、用配方法可将方程x2+2x=0变形为（ ）
A.（x+1）2=1 B.（x-1）2=1 C.（x+1）2=0 D.（x-1）2=0
8、如图，DE是△ABC的中位线，若AD＝4，AE＝5，BC＝12，
则△ADE的周长是（ ）
A．7.5 B. 15 C. 24 D. 30
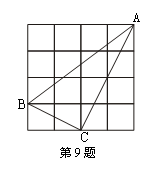9、如图正方形网格中,每个正方形的边长为1,则△ABC的
三边中,边长为无理数的边数是( )
A.0条 B.1条
C.2条 D.3条
10、在一幅长80cm，宽50cm的长方形风景画的四周镶一条
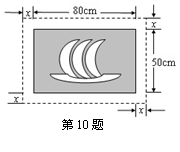金色纸边（如图所示），制成一幅新的长方形挂图.如果要
使整个新挂图的面积为7000cm2，设金色纸边的宽为xcm，
则由题意可列方程为（ ）
A．(80+2x)(50+2x)=7000 B．(80-2x)(50-2x)=7000
C．(80-2x)(50+2x)=7000 D．(80+2x)(50-2x)=7000
二、填空题(每题4分,共24分)
11、计算:
,
12、一个正n边形的内角和是540°,则n= .
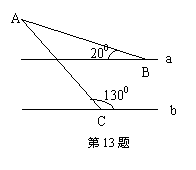
13、如图所示，直线a∥b，则∠A= 度．
14、请写出满足有一根为x=1的一个一元二次方程： .
15、如图，在菱形ABCD中，AB=5㎝，AC=8㎝，则菱形ABCD的面积为______㎝2.
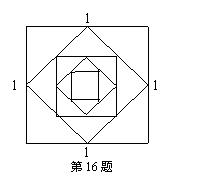
16、如图是一个边长为1的正方形，依次连接各边中点构成第一个新正方形，继续连接新正方形各边中点构成第二个新正方形，依次类推.根据下表填空：
| 第n个新正方形 | 1 | 2 | 3 | 4 | …… | n |
| 该新正方形的面积 |
|
|
|
| …… |
第n个新正方形的面积为 .
三、解答题(共46分)
17、（1）（本题5分）计算：
；
（2）（本题5分）解方程：x2＋4x－12＝O；
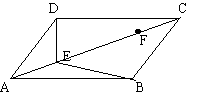18、（本题7分）如图，在平行四边形ABCD中，点E、F在对角线AC上，且AE=CF.请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）．
（1）连结___________；
（2）猜想：__________=__________.
（3）证明：
19、（本题9分）请将四个全等直角三角形(如图)，按不同要求拼成下列四边形，并在相应的方框内画出拼法示意图．
 | | | | ||||||||||
 | |||||||||||||
 | | ||||||||||||
（1）矩形 （2）菱形 （3）等腰梯形
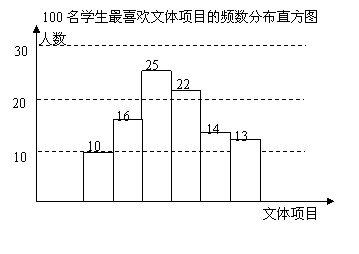
20、（本题8分）我校团委为了解800名学生课余时间喜欢的文体活动，3月份随机调查了100名学生，他们喜欢的文体项目如图所示.
（1）请估计100名学生中最喜欢田径项目的学生有 人；
（2）若随机抽查一位学生，则最喜欢音乐的概率是 ；
（3）校团委向学校建议增加球类设施，在5月份随机调查100名学生，发现喜欢球类活动人数达36人，求3月份到5月份的两个月中平均每月增加的百分率.
21、
（本题12分）如图，等腰直角三角形ABC中，∠BAC＝90°，AB=AC＝2，点P为斜边BC上的动点，PD//AC，PE//AB，设AD的长为x，请回答下列问题：
（1）当四边形ADPE为正方形，此时x= ；
（2）求当x为何值时，四边形ADPE的面积为
．
第二试（共50分）
一、选择题（每题5分，共15分）
1、已知关于x的一元二次方程
的一个根是x =1,则b+c的值是( )
A. 2 B. 1 C.0 D.-1
2、若平行四边形的一边长为５,则它的两条对角线长可以是（ ）
A.12和2 B. 4和8 C.4和6 D. 3和4
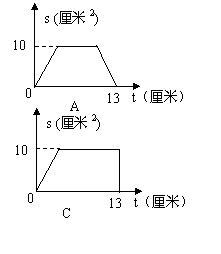
3、如图，矩形ABCD的边AB=5厘米，BC=4厘米，动点P从A点出发，在折线AD—DC—CB上以1厘米/秒的速度向B点匀速运动，那么表示△ABP的面积s(厘米2)与运动时间t（秒）之间
的关系的图象是（ ）
 |  | ||
二、填空题（每题5分，共15分）
4、当
时,代数式
的值为
.
5、如图已知：梯形ABCD中，AD∥BC，AB＝AD＝CD=2cm，BD⊥CD，则梯形ABCD的周长是__ ___cm.
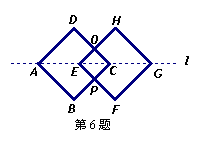6、如图，正方形
的边长为5，现沿对角线所在直线
向右平移与正方形
重合，已知四边形
的面积为4，则
的长度为
.
 |
三、解答题（共20分）
7、(本题10分) 开太百货大楼服装柜在销售中发现：“Mickey”牌童装平均每天可售出20件，每件盈利40元.为了迎接“五·一”劳动节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存.经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件.要想平均每天销售这种童装盈利1050元，那么每件童装应降价多少元？
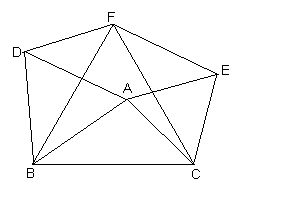
8、(本题10分)如图，△EFC是△ABC绕点C顺时针旋转60°得到的图形，△DBF是△ABC绕点B顺时针旋转60°得到的图形.
（1）请你说明四边形AEFD是平行四边形;(5分)
（2）想一想，当△ABC满足什么条件时，四边形AEFD是矩形？(3分)
（3）当△ABC满足什么条件时 ，以A、E、F、D为顶点的四边形不存在？(2分)
 |