|
八年级数学第二学期期中测试卷
一、选择题（每题3分，计36分）
1.不等式
的正整数解的个数是（ ）
A.0个 B.1个 C.2个 D.3个
2.已知一个不等式的解集在数轴上表示为如图，则对应的不等式是（ ）
A.
B.
C.
D.
3.把分式
中的x与y都扩大3倍，分式的值（ ）
A.不变 B.扩大3倍 C.缩小3倍 D.扩大9倍
4.下列分式中，与
相等的是（ ）
A.
B.
C.
D.
5.若
，则（ ）
A. m=4,n=－1 B. m=5,n=－1 C. m=3,n=1 D. m=4,n=1
6.对于直角坐标系中A（1，2）
B（2，1） C（－1，－2）
D（－2，－1）这四个点在反比例函数
的图象上的有（ ）
A.1个 B.2个 C.3个 D.4个
7.已知一次函数y=kx－2，y随x的增大而减小，那么反比例函数
（ ）
A.当x>0时，y>0 B.在每个象限内，y随x增大而减小
C.图象在第一、三象限 D.图象在第二、四象限
8.已知反比例函数（k<0）的图象上有两点A（x1,y1） B（x2,y2），且x1< x2,则
y1－y2的值是（ ）
A.正数 B.负数 C.非负数 D.不能确定
9.下列说法（1）两个全等三角形一定相似；（2）任意两个等腰直角三角形相似；（3）任意两个菱形相似；（4）任意两个正方形都相似；（5）黄金三角形都相似；其中说法正确的个数是（ ）
A.4个 B.5个 C.6个 D.7个
|
A.4个 B.5个
C. 6个 D.7个
|
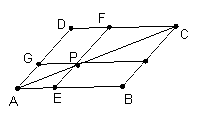
11.如图，若
，则图中相似的三角形共有（ ）
|
12.若点（－2,y1）,(1,y2), (3,y3)都在反比例函数（k<0）
的图象上，则y1，y2，y3的大小关系是（ ）
A. y1< y3< y2 B.y2 <y1<y3
C.y1<y2<y3 D.y2<y3<y1
|
2x+4>0
13.不等式组 的整数解是_____________；
1－2x>0
14.当a=_______时，分式
的值为0；
15.化简
=___________；
16.若反比例函数
的图象在第一、三象限，则函数的解析式为_______；
17.如果线段c是a,b的比例中项，且a=4,b=9，那么c=__________;
18.一棵高3m的小树的影长为4m，同一时刻临近它的一座楼房的影长是24m,这座楼高__________m；
19.如果一次函数y=(2－m)x+m的图形经过第一、二、四象限，那么m的取值范围______;
20.使分式方程
产生增根的m值是__________;
三、解答题
21.（本题12分）解不等式组，并把解集在数轴上表示出来
|
|
4x－2>2(x+1)
x－3<5－x
22.（本题8分）解分式方程
23.（本题8分）先化简
，然后取一个你喜欢的x值，求出结果。
24.（本题8分）小明买软面笔记本共用去12元，小丽买硬面笔记本共用去21元，已知每本硬面笔记本比软面笔记本贵1.2元，小明和小丽能买到相同本数的笔记本吗？
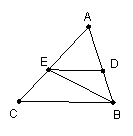
25.（本题10分）如图，在△ABC中，AD是角平分线，点E在AB上，且DEAC
|
（2）如果AB=12，AC=8，求DE的长。
26.（本题10分）如图，由边长为1的25个小正方形组成的正方形网格上有一个△ABC，请在网格上画一个顶点在小正方形的顶点，且与△ABC相似的面积最大的△A’B’C’
这样的最大三角形你最多可画几个？并求出其中一个的面积。
27.（本题12分）已知反比例函数
和一次函数
的图象都经过A（2,－1）
B(1,c)两点：（1）求两个函数解析式；（2）当x取何值时，反比例函数值大于一次函数的值。
28.（本题14分）今年6月份，我市某果农收获荔枝30吨，香蕉13吨，现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳，已知甲种货车可以装荔枝4吨和香蕉
1吨，乙种货车可装荔枝、香蕉各2吨：
（1） 该果农安排甲、乙两种货车时有几种方案？请你设计出来；
（2） 若甲种货车每辆要付运费2000元，乙种货车每辆要付运费1300元，则该果农应选择哪种方案，使运费最少？最少运费是多少？
附加题（1～3班必做）（本题10分）
先阅读下列知识，然后解答问题：
含有一个未知数，并且未知数的最高次数是2的方程，叫一元二次方程，如：
已知关于x的一元二次方程
（a,b,c表示已知量，a≠0）的解的情况是：
① 当
时，方程有两个不相等的解，方程的解为
，
；
② 当
时，方程有两个相等的解，方程的解为
③ 当
时，方程无解
解答：（1）一元二次方程
有几个解？为什么？并求出解；
（2）当a取何值时，关于x的一元二次方程
有两个不相等的解？