人教版八年级上册全等三角形单元测试试题
18中2、9班测试卷
一、复习
1．全等三角形的判定方法（四种）和直角三角形的判定方法（五种）
2．角平分线的性质和判定；角平分线可以看作和角的两边距离相等的所有的点的集合。角平分线在几何作图中的应用。
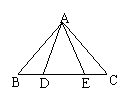
（1）已知：如图，点D、E在BC上，且BD=CE，AD=AE，求证：AB=AC
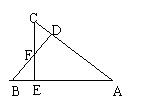
（2）已知：如图，AB=AC，BD^AC，CE^AB，垂足分别为D、E，BD、CE相交于点F，求证：BE=CD。
 | |||
 | |||
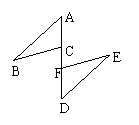（3）已知：如图。A、C、F、D在同一直线上，AF=DC，AB=DE，BC=EF，求证：AB∥DE；BC∥EF
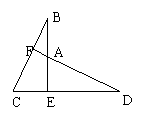（4）已知：BE⊥CD，BE=DE，BC=DA，求证：DA⊥BC.
（5）已知：如图，在△ABC中，∠C=90°，AD平分ÐBAC，（1）若BC=16，BD=10，求点D到AB的距离．（2）若BC=16，BD：CD=5：3，求点D到AB的距离．
（6）已知在△ABC中，∠A=Rt∠，AB=AC，BD是角平分线，求证：AB+AD=BC．
 |
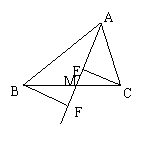（7）已知：如图，△ABC中，M是BC边上的一点，CE∥BF，CE=BF，求证：AM是BC边上的中线.
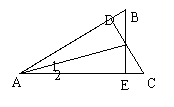
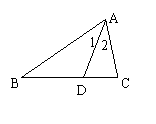（8）已知：如图，△ABC中，∠C=2∠B，∠1=∠2，求证：AB=AC+CD
（9）已知：在△ABC中，AB=AC，延长AB到D，使BD=AB，E为AB的中点，求证CD=2CE.
 |
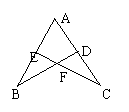（10）如图，已知BD=CE，∠B=∠C，求证：（1）AB=AC，（2）BE=CD.
（11）如图，已知∠1=∠2，∠3=∠4，求证：∠ADC=∠BCD
 |
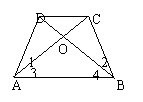（12）.已知：E是正方形ABCD的边长AD上一点，BF平分EBC，交CD于F，求证BE=AE+CF.
 |
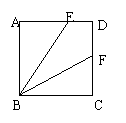