八年级
上学期期末义务教育教学质量监控监测
数学试卷（模拟卷2）
（本卷共三个大题，26个小题，考试时间120分钟满分100分）
| 题号 | 一 | 二 | 三 | 总分 |
| 得分 |
| 得分 | 评卷人 |
一、请你填一填（每小题3分，共30分）
1、小明从家走到邮局用了8分钟，然后右转弯用同样的速度走了6分钟到达书店(如右图所示)。已知书店距离邮局660米，那么小明家距离书店 米。
2、一个汽车牌在水中的倒影为 ，则该车牌照号码为
.
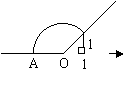3、若等腰三角形两边长分别是4cm、5cm, 则这个三角形的周长是 .
4、若正数m是小于2+
的整数，则m的值是 .
5、如右图，数轴上点A表示的数是 .
6、一个多边形的每个内角度数都是其外角度数的 2倍，则这个多边形的边数是
.
7、如右图，正方形ABCD边长为4，现沿对角线所在直线l向右平移与正方形EFGH重合，已知四边形EPCO的面积为1，则从A移到E的距离为 .
8、在平面直角坐标系内点（a,b）位于x轴上方，
y轴右侧，则a 0, b 0 .
9、已知一次函数
和两坐标轴围成的三角形的面积是10，则k = .
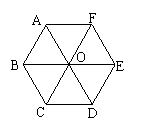
10、如图，正六边形ABCDEF对角线交于O，则图中菱形有 个；
等腰梯形有 个。
| 得分 | 评卷人 |
二、仔细选一选（每小题有且只有一个答案正确，每小题3分，共24分）
11、如右图，如果半圆的直径恰为直角三角形的一条直角边，那么半圆的面积为（ ）
A 
B 
C 
D 
12、下列说法中错误的是（ ）
A 四个角相等的四边形是矩形 B 对角线互相垂直的矩形是正方形
C 对角线相等的菱形是正方形 D 四条边相等的四边形是正方形
13、在如下案例图中，将大写字母N绕它右下侧的点按逆时针方向旋转90°，
作出旋转后的图案是（
）
 | |||||||
 | |||||||
 | |||||||
 | |||||||
案例 A B C D
14、如果点M (1-x, 1-y)在第二象限，则点N (x-1, 1-y)在（ ）
A 第一象限 B 第二象限 C 第三象限 D 第四象限
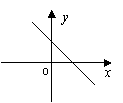
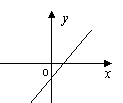
15、一次函数
的图象如右图所示，则k、b的值为（ ）
A k>0, b>0 B k>0, b<0 C k<0, b>0 D k<0, b<0
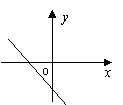
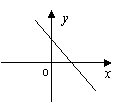
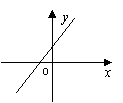16、如果ab>0, bc<0, 则一次函数
的图象的大致形状是（ ）
A B C D
17、下列图案既是中心对称图形，又是轴对称图形的是（ ）
A. B. C. D
18、若铺地面的瓷砖每一个顶点处都有六个相同的正多边形组成，则这种正多边形只能是（ ）
A．正三角形 B．正方形 C．正五边形 D．正六边形
| 得分 | 评卷人 |
三、认真思考，慎重解答
（19－21题各5分，22－25题各6分，26题7分，共46分）
19、
20、
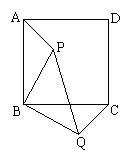21、如图P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBQ重合，若PB=3，求PQ的长。
22、读一读，想一想，做一做
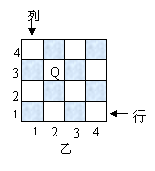
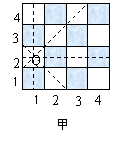
国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多：“皇后”不仅能控制她所在的行与列中的每一个小方格，而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘，图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
①在如图乙的小方格棋盘中有一“皇后Q”，她所在的位置可用“（2，3）”来表示，请说明“皇后Q”所在的位置“（2，3）”的意义，并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
②如图丙也是一个4×4的小方格棋盘，请在这个棋盘中放入四个“皇后Q”，使这四个“皇后Q”之间互不受对方控制（在图丙中的某四个小方格中标出字母Q即可）.
 | |||
 | |||
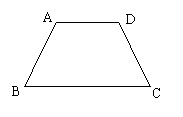
23、等腰梯形ABCD的周长为40 cm，∠B=∠C=60°，若腰长AB是8 cm，求它的上底AD的长。
 |
24、为保护环境，某样环保小组成员小明收集废电池，第1天收集1号电池4节，5号电池5节，总重量460克；第二天收集1号电池2节，5号电池3节，总重量240克，求1 号电池和5号电池每节分别重多少克？
25、某机动车出发前油箱内有42升油，行驶若干小时后，途中在加油站加油若干升。油箱中余油量Q（升）与行驶时间t（小时）之间的函数关系如图所示，根据下图回答问题：
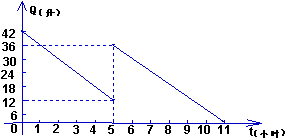(1)机动车行驶几小时后加油？答： 小时
(2)加油前余油量Q与行驶时间t的函数关系式是：
此函数自变量t的取值范围是 ；
(3)中途加油 升
(4)如果加油站离目的地还有230公里，车速为40公里/小时，要到达目的地，油箱中的油是否够用？请说明理由 .
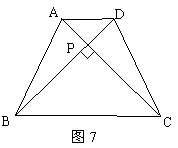
26、阅读材料：如图（6）在四边形ABCD中，对角线AC⊥BD，垂足为P.
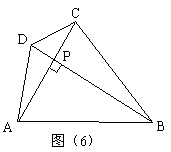因为有AC⊥BD→
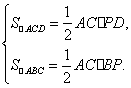所以S四边形ABCD=S△ACD+S△ACB=
=
所以S四边形ABCD=
解答问题：（1）上述证明得到的性质可叙述为:
（2）已知：如图（7），等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm,BC=7cm，利用上述的性质求梯形的面积.