湘教版八年级上学期数学测试题
一、选择题（每小题3分，共36分）
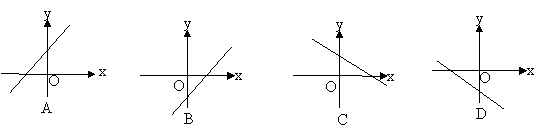1．已知正比例函数
的函数值随的增大而增大，则一次函数
的图象大致是 ( )
2、一次函数 y = x图象向下平移 2 个单位长度后，对应函数关系式是( )
A．
C．
C．
D．
3、一次函数
，经过（1，1），(2，
) ，则k与b的值为( )
A．
B．
C．
D．
4．直线y=kx+2过点（-1，0），则k的值是（ ）
A．2 B．-2 C．-1 D．1
5．和三角形三个顶点的距离相等的点是（ ）
A．三条角平分线的交点 B．三边中线的交点
C．三边上高所在直线的交点 D．三边的垂直平分线的交点
6．一个三角形任意一边上的高都是这边上的中线，则对这个三角形的形状最准确的判断是（ ）A．等腰三角形 B．直角三角形 C．正三角形 D．等腰直角三角形
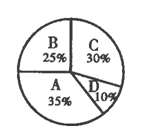
7．下图所示的扇形图是对某班学生知道父母生日情况的调查，A表示只知道父亲生日，B表示只知道母亲生日，C表示知道父母两人的生日，D表示都不知道．若该班有40名学生，则知道母亲生日的人数有（ ）
A．25% B．10
C．22 D．12
8．.如图，在△ABC中，AB= AC，D、E在BC上，BD = CE，图中全等三角形的对数为 ( ) A．0 B．1 C．2 D . 3
9.满足下列哪种条件时，能判定△ABC与△DEF全等的是( )
A．∠A=∠E ，AB = EF，∠B =∠D； B．AB=DE，BC = EF，∠C=∠F；
C．AB=DE，BC = EF，∠A=∠E； D．∠A =∠D，AB = DE，∠B=∠E
10.三峡工程在6月1日与6月10日下闸蓄水期间，水库水位由106米升至135米，高峡平湖初现人间，假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是( )
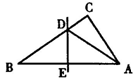
11．如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与EF交于F，若BF=AC，那么∠ABC等于（ ）
A．45° B．48° C．50° D．60°
| |
A．10cm B．12cm
C．15cm D．17cm
二、填空题（每小题3分，共18分）
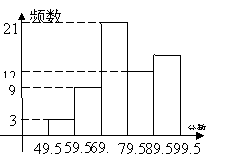
13．某市在“新课程创新论坛”活动中，对收集到的60篇”新课程创新论文”进行评比，将评比成级分成五组画出如图所示的频数分布直方图．由直方图可得，这次评比中被评为优秀的论文有_________篇。（不少于90分者为优秀）
14．线段AB = 4cm，P为AB中垂线上一点，且PA= 4cm，则∠APB =_________．
15．已知△ABC≌△DEF，若∠A=60°，∠F=90°，DE=6cm，则AC=________．
16．点P关于x轴对称的点是（3，-4），则点P关于y轴对称的点的坐标是_______．
17．已知a2+b2=13，ab=6，则a+b的值是________．
18．直线y=ax+2和直线y=bx-3交于x轴同一点，则a与b的比值是________．
三、解答题（共66分）
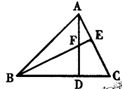
19．（8分）如图，已知PB⊥AB , PC⊥AC，且PB =PC，D 是AP上的一点，
求证：
．
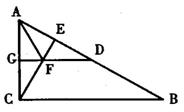
20. (8分)如图， AB = DC，AC = BD， AC、BD交于点E，过E点作EF//BC交CD于F．
求证：
。
21．（8分）求证：等腰三角形两腰上的高的交点到底边两端的距离相等．
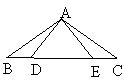
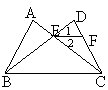
22、（10分）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，求证：（1）DF∥BC；（2）FG=FE.
23．（10分）在全国顶防某种传染病时期，某厂接受了生产一批高质量医用口罩的任务。要求在8天之内（含8天）生产A型和B型两种型号的口罩共5万只，其中A型口罩不得少于1.8万只，该厂的生产能力是：若生产A型口罩每天能生产0.6万只，若生产B型口罩每天能生产0.8万只，已知生产一只A型口罩可获利0.5 元，生产一只B型口罩可获利0.3元。设该厂在这次任务中主产了A型口罩x万只．
(l)该厂生产A型口罩可获利润_______万元，生产B型口罩可获利润______万元；
(2)设该厂这次生产口罩的总利润是y万元，试写出y关于x的函数关系式，并求出自变量x的取值范围．
(3)如果你是该厂厂长：①在完成任务的前提下，你如何安排生产A型和B型口罩的只数，使获得的总利润最大？最大利润是多少？②若要在最短时间内完成任务，你又如何来安排生产A型和B型口翠的只数？最短时间是多少？
24．（10分）某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：
| 运输工具 | 运输费单价 （元/吨·千米） | 冷藏费单价 （元/吨·小时） | 过路费 （元） | 装卸及管理费 （元） |
| 汽车 | 2 | 5 | 200 | 0 |
| 火车 | 1.8 | 5 | 0 | 1600 |
注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨小时”表示每吨货物每小时的冷藏费．
（1）设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y1（元）和y2（元），试求出y1和y2和与x的函数关系式；
（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？
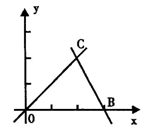
25．（12分）如图，直线OC、BC的函数关系式分别是y1=x和y2=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．
（1）求点C的坐标，并回答当x取何值时y1>y2？
（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．
（3）当x为何值时，直线m平分△COB的面积？
