19章《四边形》测试题
带※为选作题目。一、选择题（本大题8个小题，每小题4分，共32分）
1、用两块完全相同的直角三角形拼下列图形：①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形，一定能拼成的图形是（ ）A、①④⑤ B、②⑤⑥ C、①②③ D、①②⑤
2、顺次连结任意四边形四边中点所得的四边形一定是（ ）A、平行四边形 B、矩形 C、菱形 D、正方形
3、用长为100cm的金属丝制成一个矩形框子，框子的面积不可能是
A、325cm B、500cm C、625cm D、800cm
4、2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图）。如果大正方形的面积是13，小正方形的面积是1，直角三角形较短直角边为a，较长直角边为b，那么（a+b）2的值为（ ）A、13 B、19 C、25 D、169
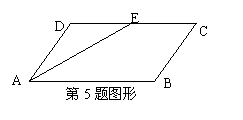5、如图，平行四边形ABCD中，∠A的平分线
AE交CD于E，AB=5，BC=3，则EC的长（ ）
A、1 B、1.5 C、2 D、3
6、等腰梯形的两底之差等于腰长，则腰与下底的夹角为（ ）A、120° B、60° C、45° D、135°
※7、在平行四边形ABCD中,∠B=110O,延长AD至F,延长CD至E,连接EF,则∠E+∠F=（ ）A、110O B、30O C、50O D、70O
※8、如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面积比是（）A.3：4 B.5：8 C.9：16 D.1：2
二、填空题（本大题6个小题，每小题3分共18分）
9、□ABCD中，∠A=50°，则∠B=__________，∠C=__________。
10、菱形ABCD的周长为36，其相邻两内角的度数比为1:5，则此菱形的面积为____________。
11、对角线长为2
的正方形的周长为___________，面积为__________。
※12、在梯形ABCD中，AD∥BC，∠A=90°，若BD=BC=DC=10，则此梯形的面积为_______。
※13、已知菱形两条对角线长分别是4cm和8cm，则它的边长为__________。
※14、□ABCD的对角线相交于点O，△AOB是等边三角形，且AB=3cm，则此平行四边形的周长为__________，面积为___________。
三、解答题（共50分）写出必要的演算过程或推理步骤。
15、（8分）已知：如图，梯形ABCD中，AD∥BC，
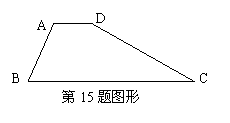∠B=60°，∠C=30°，AD=2，BC=8。求：梯形两腰AB、CD的长。
16、（8分）在直角梯形ABCD中，∠A=90°，AB∥DC，AD=15，AB=16，BC=17，求CD的长。
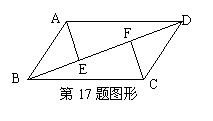17、（8分）如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：∠BAE＝∠DCF。
 |
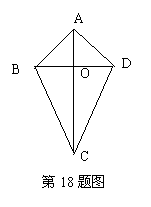18、（8分）如图，四边形ABCD中，
AC垂直平分BD于点O。
(1) 图中有多少对全等三角形？请把它们都写出来；
⑵任选（1）中的一对全等三角形加以证明。
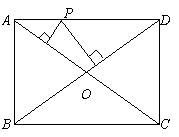
※19、（8分）如图，矩形ABCD的两边AB=3，BC=4，
P是AD上任一点，PE⊥AC于点E，PF⊥BD于点F。求PE+PF的值。
※20、（10分）已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF∥CD，分别交AB、CD、AD、BC于点M、N、E、F，设
＝PM·PE，
＝PN·PF，解答下列问题：
（1）当四边形ABCD是矩形时，见图1，请判断与的大小关系，并说明理由；
（2）当四边形ABCD是平行四边形，且∠A为锐角时，见图2，（1）中的结论是否成立？并说明理由。