八年级（08级）学月检测数学试题（三）
出题人:鲁勇军
一、填空题（每题2分，共20分）
1、下列各式中，①
, ②
, ③
, ④
，其中（填序号）
是分式
2、当x________时，分式
有意义。
3、已知：y =
，当x = ________时，y = 0。
4、若△ABC的边a、b满足
,则第三边c的中线长m的取值范围为
5、点(－3，4)到y轴的距离为____ ____个单位
6、正方形ABCD中,AC、BD交于O,∠EOF＝90o,已知AE＝3,CF＝4,则EF的长为＿＿＿.
7、若方程 
＝
+2 有增根，则 m＝_____________
8、若函数y=kx－4的图象平行于直线y=－2x，则函数的表达式是
9、有一段斜坡，某人上坡的速度为V1,下坡的速度为V2，则此人往返的平均速度为：
10、一次函数y = x - 4与y=－x＋2的图象交点的坐标是
二、选择题（每题2分，共24分）
11、下列计算正确的是（ ）
A、
B、
C、
D、
12、如果分式
中，x,y的值都变为原来的一半，则分式的值（ ）
A、不变 B、扩大2倍 C、缩小2倍 D、以上都不对
13、如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是（ ）
A．∠M＝∠N B．AB＝CD C．AM＝CN D．AM∥CN
14、下面哪个点不在函数y=－2x+3的图象上 （ ）
A、（-5，13） B、（0.5，2） C、（3，0） D、（1，1）
15、一次函数y＝kx＋b的图象经过第一、二、四象限，则有 （ ）
A、k>0,b>0 B、k>0,b<0 C、k<0,b<0 D、k<0,b>0
16、下列函数中,自变量
的取值范围不正确的是 （ ）
A 、
中,取全体实数
B、 
中,
C、 
中,≥2
D、
中, 
3
17、若y=（m—1）x
是反比例函数，则m的值为（ ）
A、 m=2 B、m=－1 C、 m=1 D、m=0
18、A(-3,a)与点B(3,4)关于y轴对称，那么a的值为( )．
A．3 B．-3 C．4 D．-4
19、如果点P(2m+1,-2)在第四象限内，则m的取值范围是( )．
A．m＞
B．m＜ C．m≥ D．m≤
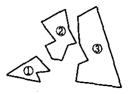
20、某同学把一块三角形的玻璃打碎也成了三块,现在要到玻
璃店去配一块完全一样的玻璃,那么最省事的办法是（ ）
A．带①去 B．带②去 C．带③去 D．带①和②去
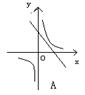
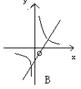
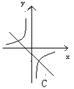
21、函数ｙ＝ｋｘ＋ｋ，
在同一坐标系中的图象大致是（ ）
22、王大爷饭后出去散步，从家中走 20 分钟到一个离家 900 米的公园，与朋友聊天10分钟后，然后用15分钟返回家里。下面图形表示王大爷离家的时间与外出距离之间的关系是（ ）
A B C D
三、计算题（每题4分，共32分）
23、计算： 
24、计算：
25、计算：
26、解方程：
27、解方程：
28、已知：
，求A和B的值
29、先化简，后求值: 
，其中
.
30、列方程解应用题：从甲地到乙地的路程是15千米，A骑自行车从甲地到乙地先走，40分钟后，B骑自行车从甲地出发，结果同时到达。已知B的速度是A的速度的3倍，求两车的速度.
四、解答题（共44分）
31、（6分）在平面直角坐标系中，描出下列各点：A（3,1），B（
）,C(
)，D
。顺次连接这四个点，求此四边形的面积。
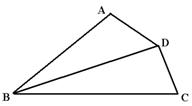32、（6分）如图,在四边形ABCD中,已知BD平分∠ABC,
∠A＋∠C＝180o,试说明AD＝CD.
33、（6分）已知y是x的反比例函数，且当x ＝ 1时y ＝４；
（1）求ｙ与ｘ的函数关系式； （2）ｘ＝４时，求ｙ的值。
（3）当x取何值时，y = 
。
34、（7分）已知一个一次函数的图象与直线y=2x+1的交点M的横坐标为2，与直线y=-x+2的交点N的纵坐标为1。
(1)求这个一次函数关系式；
(2)求这个函数图象与坐标轴围成的三角形的面积
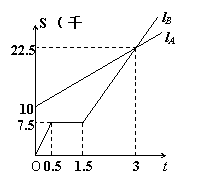
35、（8分）如图，
、
分别表示
步行与
骑车在同一路上行驶的路程
与时间
的关系。
（1）出发时与相距
千米。（1分）
（2）走了一段路后，自行车发生故障，进行修理，所用的时间是 小时。（1分）
（3）出发后 小时与相遇。（1分）
（4）若的自行车不发生故障，保持出发时的速度前进， 小时与相遇，相遇点离的出发点 千米。在图中表示出这个相遇点
（3分）
（5）求出行走的路程与时间的函数关系式。（写出过程，3分）
36、（10分）已知一次函数y＝kx＋b的图象与反比例函数
的图象相交于A、B两点，点A的横坐标为3，点B的纵坐标为 -3。
（1）求一次函数的解析式；（5分）
（2）在同一坐标系中，画出一次函数与反比例函数的图象。（注意画图的过程：列表，描点，连线）（3分）
（3）观察图象：写出当x为何值时，一次函数值小于反比例函数值？（2分）