八年级(上)期中考试数学试题
班级__________ 姓名____________ 学号___________
一、 填空题(每小题3分,共30分)
1、长方形的周长为20cm,长为xcm面积是S(cm2),则S与x的关系式是_______,其中自变量是__________,___________是_________的函数
2、函数y=![]() 中自变量x的取值范围是___________
中自变量x的取值范围是___________
3、已知一次函数y=kx+5的图象经过点(-1,2),则k=_________,y随x的增大而_________.
4、函数![]() ,当
,当![]() 时,
时,![]() 的取值范围是
的取值范围是
5、分析数据时,为了能清楚地反映事物地变化情况,可以选择________图;为了能清楚地表示出各部分在总体中所占的百分比,通常选用_______图;而为了能表示出每个项目的具体数目,我们又常选用_________图
6、如图1,在世界人口扇形统计图中,关于中国部分的圆心角的度数为 度
 7、已知△ABC≌△A′B′C′,A与A′,B与B′是对应顶点,△ABC的周长为12cm,AB=3cm,BC=4cm,则A′C′=_____cm
7、已知△ABC≌△A′B′C′,A与A′,B与B′是对应顶点,△ABC的周长为12cm,AB=3cm,BC=4cm,则A′C′=_____cm

图1 图2 图3
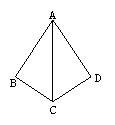
8、如图2所示,∠B=∠D=90°,要证明△ABC与△ADC全等,还需要添加的一个条件(只需添加一个)是______________________,根据是_______________
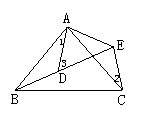
9、如图3所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____
10、小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表
二、选择题(每小题2分,共20分)
1、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,自变量是( )
 A、沙漠
B、体温 C、时间 D、骆驼
A、沙漠
B、体温 C、时间 D、骆驼
2、一次函数![]() 的图象经过( )
的图象经过( )
A、第一、三、四象限 B、第二、三、四象限
C、第一、二、三象限 D、第一、二、四象限
3如图MB=ND,∠MBA=∠NDC,下列条件中不能判定⊿ABM≌⊿CDN的是( )
A、∠M=∠N B、AB=CD C、AM=CN D、AM∥CN
4、下列条件:①AB=A′B′,BC=B′C′,AC=A′C′; ②∠A=∠A′,∠B=∠B′,∠C=∠C′;
③AB=A′B′,BC=B′C′,∠C=∠C′; ④AB=A′B′,∠B=∠B′,∠C=∠C′
其中不能说明△ABC和△A′B′C′全等的有( )
A、1个 B、2个 C、3个 D、4个
5、AD是△ABC的角平分线,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )
A、DE=DF B、BD=CD C、AE=AF D、∠ADE=∠ADF
6、函数y=kx+b的图像与函数![]() 的图像平行,且与y轴的交点为M(0,2),则其函数表达式为( ).
的图像平行,且与y轴的交点为M(0,2),则其函数表达式为( ).
A、y=![]() x+3
B、y=
x+3
B、y=![]() x+2
C、y=-
x+2
C、y=-![]() x+3 D、y=-
x+3 D、y=-![]() x+2
x+2
7、若直线y=2x+3与y=3x-2b相交于x轴上,则b的值是( ).
A、b=-3 B、b=-![]() C、b=-
C、b=-![]() D、b=6
D、b=6
8、已知在一个样本中,50个数据分别落在5个小组内,第一、二、三、五组数据分别为2,8,15,5,则第四小组的频数和频率分别为( )
A、25,0.5 B、20,0.5 C、20,0.4 D、25,0.4
9点P1(-3,y![]() ),点P2(2.y
),点P2(2.y![]() )是一次函数y=-4x + 3 图象上的两个点
)是一次函数y=-4x + 3 图象上的两个点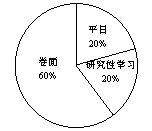 ,y
,y![]() 与y
与y![]() 的大小关系是( ).
的大小关系是( ).
A、y![]() >y
>y![]() B、y
B、y![]() >y
>y![]() > 0 C、y
> 0 C、y![]() <y
<y![]() D、y
D、y![]() =y
=y![]()
10、小明根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还。”如果用纵轴y表示父亲与儿子行进中离家的距离,用横轴x表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是 ( )
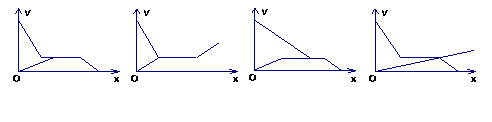
A B C D
三、解答题
1、已知一次函数y=kx+b的图象经过点A(-2,-3)及点B(1,6)
(1)求此一次函数的解析式。
(2)求此函数图象与坐标轴围成的三角形的面积。(6分)
2、观察下列大棚蔬菜种植情况统计图,回答问题:
⑴填上扇形统计图中括号中的数据;
 ⑵哪种蔬菜种植面积最大?
⑵哪种蔬菜种植面积最大?
⑶哪两种蔬菜种植面积较接近?
(4)已知豆角种了27公顷,种植蔬菜的总面积是多少公顷?种植西
红柿多少公顷?(8分)
3、已知:如图,![]() 、
、![]() 、
、![]() 、
、![]() 四点在一直线上,
四点在一直线上,![]() ,
,![]() ∥
∥![]() ,且
,且![]() .
.
请问图中有哪几对全等三角形?并任选其中一对给予证明。(8分)
 |

4、某社区要调查社区居民双休日的学习状况,采用下列调查方式:
①从一幢高层住宅楼中选取200名居民;
②从不同住宅楼中随机选取200名居民;
③选取社区内200名在校学生.
⑴上述调查方式最合理的是_____________________;
⑵将最合理的调查方式得到的数据制成扇形统计图(如图1)和频数分布
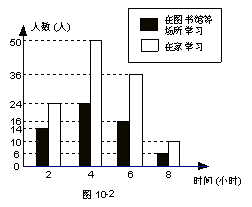 直方图(如图2).在这个调查中,200名居民双休日在家学习的有____________人;
直方图(如图2).在这个调查中,200名居民双休日在家学习的有____________人;
⑶请估计该社区2 000名居民双休日学习时间
不少于4小时的人数.(8分)
5、已知函数y![]() =x-1和y
=x-1和y![]() =-2x+3
=-2x+3
(1)在直角坐标系中画出这两个函数的图象
(2)求这两个函数的交点坐标
(3)观察图象,当x在什么范围内时,y![]() >y
>y![]() (6分)
(6分)
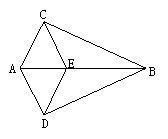 6、如图所示,∠ACB=∠ADB=90°,AC=AD,E在AB上,
6、如图所示,∠ACB=∠ADB=90°,AC=AD,E在AB上,
求证:(1)点A在∠CBD的平分线上.(2)CE=DE.(8分)
7、某车间有20名工人,每人每天加工甲种零件5个或乙种零件4个,在这20名工人中,派x人加工甲种零件,其余人加工乙种零件,已知每加工一个甲种零件可获利16元,每加一个乙种零件可获利24元.
(1)写出此车间每天所获利润y(元)与x(人)之间的函数关系式.
(2)若要使车间每天获利不低于1800元,问至少应派多少人加工乙种零件.(6分)