八年级（上）十月份月考数学试题
命题人 戴继铭
一、 填空题：请在下列空格中，仔细思考后填写（每小题3分共30分）
1．如图，直线DE交AB，AC于D,E. 
则
_____.
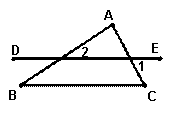
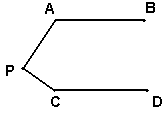
(第1题) (第2题)
2．如图, AB∥CD, 
则
__________.
3．等腰三角形的顶角是
，则它的腰上的高与底边的夹角为_________.
4．直角三角形中,两个锐角的平分线所夹的钝角是___________度.
5．直角三角形的两条直角边分别为5CM和12CM,那么这个直角三角形斜边上的中线长为_______CM.
6．一名滑雪运动员沿着倾斜角为
的斜坡,从A处滑到B处,这名滑雪运动员的高度下降了120米,问该运动员滑行了_______米
7．如图,△ABC中,
与
的平分线相交于点O,过O作EF∥BC,交AB,AC于E,F. 若AB=7,BC=5,AC=6,则△AEF的周长是__________.
8．将一条两边互相平行的纸带按如图折叠,
,则
_________.
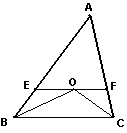
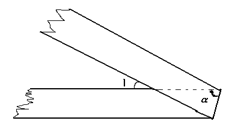
(第7题) (第8题)
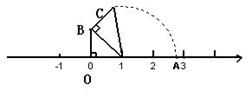
9．如图,OB=BC=1.数轴上点A表示的数是_________.
10．直角三角形斜边长为2,周长为
,则该直角三角形面积是___________.
 |
(第9题) (第11题)
二、 选择题:四个选一个,请你对下列各题作出明智的选择(每小题3分,共24分)
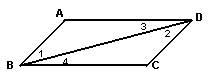
11．如图,能判定AD//BC的条件是 ( )
A. 
B.
C.
D.
12．两条直线被第三条直线所截,有一对同旁内角互补,则这对同旁内角的角平分线( )
A.互相平行 B.相交但不垂直 C.互相垂直 D.不能确定
13．等腰三角形一边长为3,另一边长为7,则它的周长为 ( )
A.10 B.13 C.17 D.13或17
14．一个等腰三角形的腰长为4,底边上的高为2,则它的顶角为 ( )
A.
B.
C.
D.
15．等边三角形的对称轴有几条 ( )
A.1条 B. 2条 C. 3条 D.无数条
16．下列各组数中,不能构成直角三角形三边的一组数是 ( )
A. 1 2 
B. 2 7 
C.
3 4 5 D. 3 4 
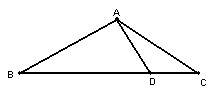
17．△ABC中,AB=AC, 
,
AD=3,则BC的长为 ( )
A. 12 B. 9 C. 8 D. 6
(第17题) (第18题)
18．如图,一架25分米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端C的距离为7分米.如果梯子的底部向外移动8分米,那么梯子顶端A将下落多少分米 ( )
A.8分米 B. 7分米 C. 1分米 D.4分米
三、尽情发挥你的能力,请解答下列各题 (共46分).
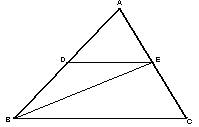
19. (本题6分)如图,已知BE平分,
.
㈠DE与BC是否平行,请说明理由.
㈡当
时,求
的度数.
(第19题)
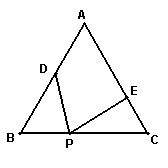20. (本题8分)如图, △ABC中,AB=AC,BP=CE,BD=CP.
㈠当
时,求
的度数.
㈡当
时,用含
的代数式表示.
21. (本题6分)等边三角形给人以“稳如泰山”的美感它具有独特的对称性，请你用三种不同的分割方法，将下列三个正三角形分别分割成四个等腰三角形.(在图中画出分割线,并标出必要的角的度数)
22. (本题6分)已知一个等腰三角形的三边分别是
那么这个三角形的周长是多少?
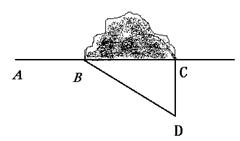23. (本题8分)某山区要修建一条高速公路,如图.在施工过程中要沿直线AB打通一条隧道。动工前测得
,BD=32Km,请你根据上述数据,求出隧道BC的长(精确到0.1Km).
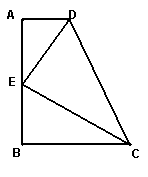24. (本题8分) 如图,AD//BC, 
,E是AB上一点,且AE=BC,
.
㈠AD与BE相等吗?请说明理由.
㈡△DEC是不是直角三角形,请说明理由.
25.(本题4分) 如图，△ABC中∠BAC=90°，AB=AC，D是斜边BC的中点，E，F分别是AB，AC边上的点，且DE⊥DF，若BE=12，CF=5，求△DEF的面积。
