八年级（下）数学期末检测题一
班级__________姓名_________________
一、填空题（每小题2分，共20分）
1．当x 时，分式
无意义；当
时,分式
的值为零
2．各分式
的最简公分母是_________________
3．点A是反比例函数图象上一点，它到原点的距离为10，到x轴的距离为8，则此函数表达式可能为_________________
4．已知
与
互为相反数，则以x、y、z为边的三角形是 三角形。（填“直角”、“等腰”、“任意”）
5．有一棵9米高的大树，树下有一个1米高的小孩，如果大树在距地面4米处折断（未折断），则小孩至少离开大树___________米之外才是安全的。
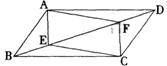
6．如图，E、F是□ABCD对角线BD上的两点，请你添加一个适 当 的条件：___________，使四边形AECF是平行四边形。
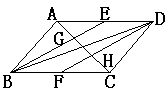7．如图，在□ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于G、H，试判断下列结论：①ΔABE≌ΔCDF；
②AG=GH=HC；③EG=
④
，其中正确的结论是_________个
8．如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，这痕为PQ，则PQ的长为_______。
9．已知：在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD,AD=3cm,BC=7cm,则梯形的高是_______cm
10．小林在初三第一学期的数学书面测验成绩分别为：平时考试第一单元得84分，第二单元得76分，第三单元得92分；期中考试得82分；期末考试得90分.如果按照平时、期中、期末的权重分别为10%、30%、60%计算，那么小林该学期数学书面测验的总评成绩应为__________分。
二、选择题（每小题3分，共30分）
1．计算
的结果是（ ）
A．
B．
C．
D．
2．成人体内成熟的红细胞的平均直径一般为0.m保留三个有效数字的近似数，可以用科学记数法表示为（ ）
A．
B．
C．
D．
3．反比例函数图像经过点P(2,3)，则下列各点中，在该函数图像上的是（ ）
A．
B．
C． (6,1) D．
4．若分式方程
有增根，则
的值为（ ）
A．4 B．2 C．1 D．0
5．已知一直角三角形的木板，三边的平方和为1800cm2,则斜边长为（ ）.
A．80cm B．30cm C．90cm D．120cm.
6．下列说法中，正确的个数有（ ）
①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为
；
②直角三角形的最大边长为
，最短边长为1，则另一边长为
；
③在△ABC中，若∠A:∠B:∠C＝1：5:6，则△ABC为直角三角形；
④等腰三角形面积为12，底边上的高为4，则腰长为5。
A．1个 B．2个 C．3个 D．4个
7．已知四边形ABCD的对角线相交于O，给出下列 4个条件： ①AB∥CD， ②AD∥BC；
③AB=CD， ④∠BAD=∠DCB，从以上4个条件中任选 2个条件为一组，能推出四边形ABCD为平行四边形的有（ ）
A．6组 B．5组 C．4组 D．3组
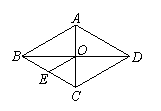
8．已知：如图，菱形ABCD中，对角线AC与BD相交于点O，
OE∥DC交BC于点E，AD＝6cm，则OE的长为（ ）
A．6 cm B．4 cm C．3 cm D．2 cm
9．能判定四边形是平行四边形的条件是（ ）
A、一组对边平行，另一组对边相等 B、一组对边相等，一组邻角相等
C、一组对边平行，一组邻角相等 D、一组对边平行，一组对角相等
10．在一次科技知识竞赛中，两组学生成绩统计如下表，通过计算可知两组的方差为
，
。下列说法：①两组的平均数相同；②甲组学生成绩比乙组学生成绩稳定；③甲组成绩的众数＞乙组成绩的众数；④两组成绩的中位数均为80，但成绩≥80的人数甲组比乙组多，从中位数来看，甲组成绩总体比乙组好；⑤成绩高于或等于90分的人数乙组比甲组多，高分段乙组成绩比甲组好。其中正确的共有（
）.
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人 数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
A．2种 B．3种 C．4种 D．5种
三、解答题（共50分）
1．当
时，求
的值。（6分）
2．便民服装店的老板在上海看到一种夏季衬衫，就用8000元购进若干件，以每件58元的价格出售，很快售完，又用17600元购进同种衬衫，数量是第一次的2倍，每件进价比第一次多了4元，服装仍按每件58元全部售完，问该服装店这笔生意赢利多少元？(7分)
3.（7分） 如图，已知直线
与
轴、
轴分别交于点A、B，与双曲线
（<0）分别交于点C、D，且C点的坐标为（
，2）.
⑴分别求出直线AB及双曲线的解析式；
⑵求出点D的坐标；
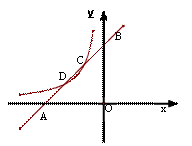⑶利用图象直接写出：当x在什么范围内取值时，
>
.
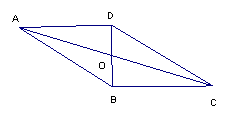4.（7分）如图，□ABCD中，BD⊥AD，AD=6cm，□ABCD的面积为24
，求□ABCD的周长及BD、AC的长。(6分)
5．（7分）如图，在梯形ABCD中，AD∥BC,AB=CD,延长CB到E，使EB=AD,连接AE，
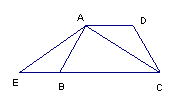求证：AE=AC
6．（8分）如图，在梯形ABCD中，AB∥DC,AD=DC=CB,AD和BC的延长线相交于G,CE⊥AG于E,CF⊥AB于F
（1）请写出图中4组相等的线段，（已知的相等线段除外）
（2）选择（1）中你所写的一组相等是线段，说明它们相等的理由。
7．(8分)张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”，对两位同学进行了辅导，并在辅导期间进行了10次测验，两位同学测验成绩记录如下表：
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 | |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
利用表中提供的数据，解答下列问题：
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | 80 |
（1）填写完成下表：
（2）张老师从测验成绩记录表中，求得王军10次测验成绩的方差
=33.2，请你帮助张老师计算张成10次测验成绩的方差
；
（3）请你根据上面的信息，运用所学的统计知识，帮助张老师做出选择，并简要说明理由。