八年级（下）数学期末试卷

八年级（下）数学期末试卷

班级　　　  姓名　　　　　   成绩　　　　 

一、填空题（每空1分，共17分）．

1．设a＞b，则　　　；　　　　　　 （m < 0）．

2．的公因式是　　　　　　　 ．

3．若是完全平方式，则 k =　　　　　　　  ．

4．已知：线段，，则、的比例中项　　　　  ．

5．分式方程+1=有增根，则m=　　　　 ．

6．若，则不等式的解集是：　　　　　　　 ．

7．已知，则A =　　　　，B =　　　　．

8．若△ABC∽△DEF，且∠A = 50°，∠E = 70°，则∠C　= 　　　　°；如果AB = 3，DE = 4，且S_△ABC = 18，则S_△DEF =　　　　　  ．

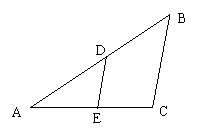
9．如图1，要使△AEF∽△ACB，已具备的条件是　　　　  　　　　，还需补充的直接条件是　　　　　　　　 （只要填写一个满足要求的条件即可）．

（图1）　　　　　　　　　　　　　　　 （ 图2）

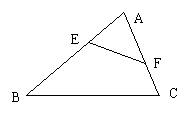
10．如图2，△ABC∽△ADE，，则　　　　　 ，　　　　　 ，　　　　  ．

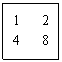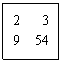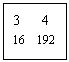11．如图3，正方形内的数有相同的规律，请找出这一规律，推算出　　　　　 ．

（图3）

二、选择题（每题2分，共14分）．

12．不等式的正整数解的个数是(　　　 ) ．

A．1个

B．3个

C．4个

D．无数个

13．关于x的方程的解为x = 1，则a =（　　　 ）．

A．1

B．3

C．

D．

14．不等式组的解集是x<2，则的取值范围是（　　　）．

A．

B．

C．

D．无法确定

15．兴趣小组想用铁丝围成两个面积相同的圆和正方形，已知它们分别用L1和L2长度的铁丝，则（　　  ）．

A． L1 < L2

B．L1 = L2

C． L1 > L2

D．无法确定

16．下列语句不是命题的是（　　　）．

A．今天的天气是晴转阴	B．过直线外一点A作AB∥
C．两点之间线段最短	D．如果，则

17．下列命题：①邻补角的角平分线互相垂直；

②如果两直线平行，那么同位角的平分线互相平行；

③内错角相等；

④如果，，则．

其中是真命题的个数是（　　　）．

A．1

B．2

C．3

D．4

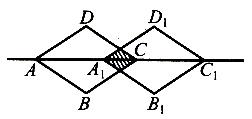18．如图4，把菱形沿着对角线的方向移动到菱形的位置，它们的重叠部分（图中阴影部分）的面积是菱形的面积的，若，则菱形的移动距离是（　　  ）．　　　　　　　　　　　 （图4）

A．

B．

C．1

D．

三、求值并作图（第19题5分，第20、21题每题6分，共15分）．

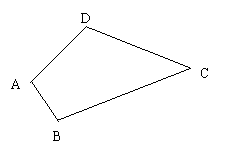19．如图5，四边形ABCD．以点C为位似中心作四边形ABCD的位似图形，且四边形ABCD与四边形的位似比为2 : 1．

（图5）

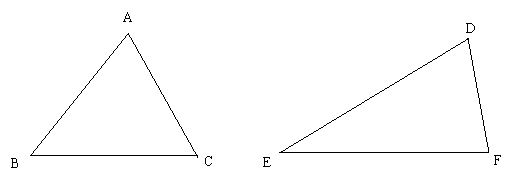
20．如图6，在和中，已知，，．画直线，，使直线将分成两个小三角形，使直线将分成两个小三角形，并使分成的两个小三角形分别与分成的两个小三角形相似，并标出每个小三角形各个内角的度数（画图工具不限，不要求写画法）．

（图6）

人数

21．为制定本市初中七、八、九年级学生校服的生产计划，有关部门对180名初中男生的身高作了调查，调查结果如下表：

	七年级	八年级	九年级	总数 (频数)
143~153	12	3	0
153~163	18	9	6
163~173	24	33	39
173~183	6	15	12
183~193	0	0	3

（注：每组可含最低值，不含最高值）

（1）根据表中的数据完成表中的空格；

（2）绘制频数分布直方图（要体现每个年级的人数）．

四、化简或求解（集）题（每题4分，共24分）．

22．把下列各式分解因式．

（1）；

（2）．

23．解下列不等式（组），并把解集在数轴上表示出来．

（1）；

（2）

24．化简或解方程．

（1）．

（2）．

五、解答或证明题（第25、26题每题6分，第27、28题每题8分，共28分）．

B

A

25．已知：如图7，AE、CE分别平分∠BAC、∠ACD，且∠CAE与∠ACE互余．

求证：AB∥CD．

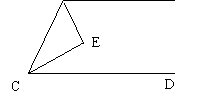
（图7）

26．在绿茵场上，足球队员带球进攻，总尽可能向球门冲（如图8），请你用所学的知识说说这是为什么？

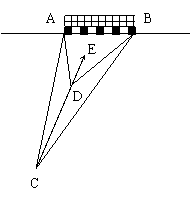（图8）

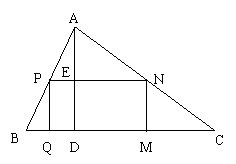27．如图9，把一个三角形余料加工成矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，且PN = 2PQ．若这块三角形余料的边BC = 12cm ，高AD = 8cm，则这个矩形零件的长和宽各是多少？

（图9）

28．如图10，在中，，，点从点开始沿线段边向点以2cm/s的速度移动，点Q从点B开始沿线段BC边向点C以3cm/s的速度移动，如果P、Q分别从A、B同时出发，经过几秒钟△PBQ与△ABC相似？

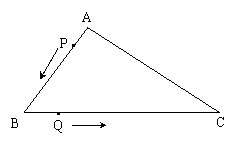（图10）