肇庆市2003—2004学年度第二学期期末水平测试试题
八年级数学科
一、填空题:(每空格1分,共12分)
1、分解因式:(1)![]() =
;(2)
=
;(2)![]() =
=
2、要使分式![]() 无意义的x的取值是
。
无意义的x的取值是
。
3、在比例尺1:10000的肇庆市城区地图上,牌坊广场与肇庆火车站的距离约是30cm,则它们之间的实际距离约为 千米。
4、计算:![]() =
=
5、位似图形上某一对对应点到位似中心的距离分别为4cm和8cm,则它们的位似比为 。
6、当x= 时,分式![]() 与分式
与分式![]() 的值相等。
的值相等。
7、若![]() 是一个完全平方式,则k的值是
。
是一个完全平方式,则k的值是
。
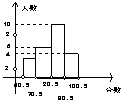 8、小明身高是1.5米,他的影长是2米,同一时刻一电线杆的影长是20米,则电线杆的高度是
米。
8、小明身高是1.5米,他的影长是2米,同一时刻一电线杆的影长是20米,则电线杆的高度是
米。
9、我市某校八年级的数学竞赛小组进行了一次数学测验,如图1是反映这次测验情况的频率分布直方图。那么该小组共有 人;80.5~90.5这一分数段的频率是 。
10、当x 时,一次函数![]() 的值大于
的值大于![]() 的值。
的值。
 二、选择题:(每小题2分,共10分)
二、选择题:(每小题2分,共10分)
11、若![]() ,则下列不等式中错误的是( )
,则下列不等式中错误的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12、把分式![]() 中的a、b都扩大2倍,则分式的值( )
中的a、b都扩大2倍,则分式的值( )
(A)扩大4倍 (B)扩大2倍 (C)缩小2倍 (D)不变
13、如图2,直线a、b与直线c相交,给出下列条件:①∠2=∠3;②∠1=∠4;③∠1+∠4=1800。则其中能判断a∥b的是( )
(A)①②③ (B)①② (C)①③ (D)只有①
14、已知![]() ,则
,则![]() 的值为( ) (A)
的值为( ) (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
15、不等式![]() 的负整数解集是( )
的负整数解集是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() ,
,![]() (D)
(D)![]() ,
,![]() ,0
,0
三、计算下列各题:(每小题4分,共8分)
16、 ![]() 17、
17、 ![]()
四、解答下列各题:(每小题4分,共12分)
18、解不等式![]() 19、 因式分解:
19、 因式分解:![]()
并把它们的解集在数轴上表示出来。

20、如图3,你能比较∠1与∠2的大小吗?请说明理由。

五、(本题满分6分)
21、如图4,△ABC中,∠A=460,CE是∠ACB的平分线,B、C、D在同一直线上,FD∥EC,∠D=420,
求证:∠B=500
六、(本题满分6分)
22、某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
李超:2.50,2.42,2.52,2.56,2.48,2.58
陈辉:2.54,2.48,2.50,2.48,2.54,2.52
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
七、(本题满分7分)
23、如图5,已知△ABC中,AB=12,BC=8,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和以A、B、C为顶点的三角形相似,且相似比为![]() 。
。
(1)根据题意确定D、E的位置,画出简图;
(2)求AD、AE和DE的长。
八、利用方程或不等式的知识解决以下问题(共9分)
24、为了开发鼎湖风景区,需要修一条长为1000米的大道,实际施工时每天的
工效比原计划增加25%,结果提前10天完成,原计划每天修路多少米?(4分)
25、我市某单位组织员工到星湖租船游玩,现有如下信息:如果每船坐6人,就剩下18人;如果每船坐10人,就有一只船不空也不满,根据以上信息确定有多少只船及参加游玩的员工人数。