八年级上系列第二章《实数》测试
总分：１２０分 姓名 成绩
一、
选择题。（共30分，10×3）。
1，下列各数：3.141592，—
，0.16，
，
，
，
，
，
是无理数的有（ ）个。
A, 2 B,3 C ,4 D,5
2,
的算术平方根是（ ）
A ,4 B,±4 C ,2 D,±2
3, 边长为2正方形的对角线长是（ ）
A. 整数 B. 分数 C. 有理数 D. 不是有理数
4, 
的平方根是（ ）
A、－6 B、36
C、±6 D、±
5,下列说法正确的是（ ）
A,
没有意义；B.负数没有立方根；C.平方根是它本身的数是0，1；
D.数轴上的点只可以表示有理数。
6，下列等式中：①，
②，
③，
④，
=0.001 ⑤， 
⑥， 
⑦，（—
）２＝２５中正确的有（ ）个。
A,2 B ，3 C，4 D.5
7，下列说法错误的是（ ）
A, 
是2的平方根；B，两个无理数的和，差，积，商仍为无理数；C，—２７的立方根是—３；D，无限小数是无理数。
８，下列计算正确的是（ ）。
A, ＋＝；B,
；C，
；D，
９，若规定误差小于1, 那么
的估算值为(
)
A. 3 B. 7 C. 8 D. 7或8
１０，圆的面积增加为原来的n倍，则它的半径是原来的（ ）。
A,n倍； B,
C,
倍 D,２n倍。
二．填空题。（每空1.5分，共24分）。
１，请你任意写出三个无理数： ；
２，
的平方根是 ；
的平方根是
３，计算：
＝ ；
４，
. 
, 
= .
５，一个直角三角形的两直角边分别为2，3。则它的斜边长为 ；如果结果精确到0.01，则约为 ；
6，满足
的整数
是
.
7，┃１－┃＝ .
8，若一个正数的平方根是
和
，则
，这个正数是 ；
9，如果
的平方根等于
，那么
；
10，若
，则
；
11，比较大小:
;
.(填“>”或“<”)
12，工人师傅要在一块面积为20m2的正方形的地面上铺地板，试估计这块地面的边长约为
m(误差小于0.1m).
三，计算题。（共66分）。
1， 求下列χ的值。（9分）。
①，16χ2—9=40
②，
③，
2，计算（32分）①，
②，
③，
④，
⑤
⑥
⑦，
⑧，请在同一个数轴上作出
和的对应的点。
四，已知长方形的长与宽的比为3∶2，对角线长为
cm，求这个长方形的长与宽。（精确到0.01cm）（4分）。
五，两位同学在打羽毛球, 一不小心球落在离地面高为6米的树上. 其中一位同学赶快搬来一架长为7米的梯子, 架在树干上, 梯子底端离树干2米远, 另一位同学爬上梯子去拿羽毛球. 问这位同学能拿到球吗?（5分）。
六，自由下落的物体的高度
(米)与下落时间
(秒)的关系为=4.9
.有一学生不慎让一个玻璃杯从19.6米高的楼上自由下落, 刚好另有一学生，站在与下落的玻璃杯同一直线的地面上, 在玻璃杯下落的同时楼上的学生惊叫一声. 问这时楼下的学生能躲开吗? (声音的速度为340米/秒)。（5分）。
七，如图所示，要在离地面5米处的电线杆上的两侧引拉线AB和AC，固定电线杆，两根拉线与地面都成60°角，现有长10.8米的一根金属线，用这根金属线能否做成符合要求的两根拉线？（5分）。
八，如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点就做格点，以格点为顶点分别按下列要求画三角形；
①，使三角形的三边长分别为2，3，
（在图①中画出一个既可）；（2分）
②，使三角形为钝角三角形且面积为4（在图②中画出一个既可），并计算你所画三角形的三边的长。（4分）。
 |  |
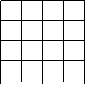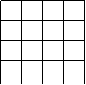① ②
 | | ||||
 | |||||