巢湖市二中八年级数学（上）期中考试试卷
 |
（时间：约120分钟 满分：120分）
一、填空题（每题4分，计32分）
1、
；
；
2、用长5cm,宽4cm的邮票80枚不重不漏摆成一个正方形，这个正方形的边长等于________cm。
3、大于
且小于
的所有整数是_______________。
4、比较大小
______ 
。
5、已知直角三角形的二边分别为5、12、则第三边长为
。
6、钟表上的分针绕其轴心旋转,分针经过15分钟后,分针转过的角度是 ；
7、对角线长为2cm的正方形的面积是
；
8、如图，AD‖BC, AB‖CD, 要使四边形ABCD为菱形还需添加的条件是 ；
二、选择题（每题4分，计32分）
1、. 在下列各数中是无理数的有…………………………………………………………【 】
-0.333…,
, 
, 
, 3
, 3.1415, 2.010101…(相邻两个1之间有1
个0),76.…(小数部分由相继的正整数组成).
A.3个 B.4个 C. 5个 D. 6个
2、下列说法中正确的有……………………………………………………………………【 】
①
都是8的立方根，②
，③
的平方根是3，④-
（A）1个 （B）2个 （C）3个 （D）4个
3、 下列说法正确的是……………………………………………………………………【 】
A、平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B、平移和旋转的共同点是改变图形的位置
C、图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D、由平移得到的图形也一定可由旋转得到
4、下列四个图形中，不能通过基本图形平移得到的是…………………………………【 】
 |
5 、平行四边形ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）
A．1：2：3：4 B. 3：4：4：3 C. 3：3：4：4 D. 3：4：3：4
6、化简：
得………………………………………………【 】
A、－1 B、
C、
D、
7、平行四边形的一条边长是10，则两条对角线的长可以是…………………………【 】
A、4或8 B、6或8 C、8或10 D、10或12
8、矩形、菱形、正方形读都有的性质是……………………………………【 】
A、对角线相等； B、对角线平分一组对角 C、 对角线互相平分 D、对角线互相垂直
三、做一做
1、化简与计算（每题5分，计10分）
(1)
（2）
2、（本题8分）已知：x=
,y=
. 求：x2 + xy + y2的平方根
四、试一试
1、（本题8分）我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x 轴于点A”，请根据图形回答下列问题：
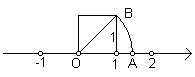（1）线段OA的长度是多少？（要求写出求解过程）（3分）
（2）作这样的图目的是为了说明什么？（3分）
（3）这种研究和解决问题的方式，体现了 的数学思想方法。（2分）
（将下列符合的选项序号填在横线上）
A、数形结合 B、代入 C、换元 D、归纳
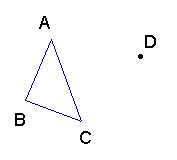2、（本题8分）△ABC绕点C旋转后，顶点A的对应点为点D，试确定顶点B对应点E的位置，以及旋转后的△DEC
3、（本题9分）如图，四边形ABCD是平行四边形，对角线AC、BD相交于O。
（1）如果∠ABC = 40º，求∠ADC，∠BCD的度数。
（2）如果AD=20，AC=18，BD=26，求△OBC的周长。
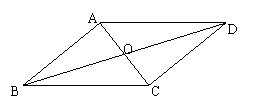（3）如果AB=10，Ac=12，Bd=16，这个平行四边形是菱形吗？为什么？
五、创新题（本题13分）
3、如图，正方形ABCD的边长为1，AB、AD上各有一点P、Q，△APQ的周长为2，求∠PCQ
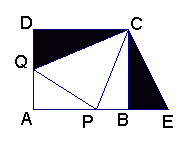为了解决这个问题，我们在正方形外以BC和AB延长线为边作△CBE，使得△CBE≌△CDQ（如图）
⑴△CBE可以看成由△CDQ怎样运动变化得到的？（2分）
⑵图中PQ与PE的长度有什么关系？为什么？（3分）
⑶请用（2）的结论证明△PCQ≌△PCE（2分）
⑷根据以上三个问题的启发，求∠PCQ的度数。（2分）
⑸对于题目中的点Q，若Q恰好是AD的中点，求BP的长。（4分）
友情提示：请同学们做完后仔细的检查一下，祝你考出好成绩。
命题人：黄志平