八年级(上)数学期末测试题(一)
班级_________ 姓名_________ 学号_______
一、选择题（每小题3分，共30分）
1、下列计算正确的是（ ）
A、3a+2b=5ab B、5y2-2y2=3 C、-p2-p2=-2p2 D、7m-m=7
2、计算（3x+9）(2x-5)等于（ ）
A、5x2+3x-45 B、6x2-3x+45 C、5x2+3x+45 D、6x2+3x-45
3、下列几何图形中，是轴对称图形而不是中心对称图形的是（ ）
A、等腰三角形 B、三角形 C、直角三角形 D、圆
4、下列计算不正确的是（ ）
A、(x-1)(-1-x)=1-x2 B、x3+4x3=5x3 C、(x+1)2=x2+1 D、(-3a5)2÷(a2)3=9a4
5、函数y=x0+
的自变量x的取值范围为（ ）
A、x≥0 B、x＞0 C、x＝0 D、x≠0
6、若一次y=kx+b的图象经过点(-2,-1)和(1,2)，则这个函数的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
7、无论a、b为何值，代数式2ab-a2-b2-1的值一定为（ ）
A、正数 B、负数 C、非正数 D、非负数
8、具有下列条件的两个等腰三角形，不能判断它全等的是（ ）
A、顶角、一对腰相等 B、底边、一腰对应相等
C、两腰对应相等 D、一底角、底边对应相等
9、下列说法正确的是（ ）
A、如果两条直线互相垂直平分，那么这两条直线互为对称轴
B、如果两个图形关于直线对称，那么它们的对应线段的长度相等
C、如果两个三角形一模一样，那么它们形成了轴对称图形
D、如果两个图形关于某直线对称，那么对称点一定在这条直线的两旁
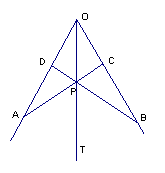
10、如图，OT是∠AOB的平分线，且OD=OC，AC与BD交于OT上点P，则图中全等三角形有（ ）
A、4对 B、3对 C、2对 D、1对
二、填空题（每小题3分，共24分）
11、因式分解：-a3b2+2a2b3-ab4等于_____________
12、点A（1，m）在函数y=2x的图象上，则点A关于y轴的对称点的坐标是_____________。
13、若x2+2xy+y2-a(x+y)+25是完全平方式，则a的值为______________。
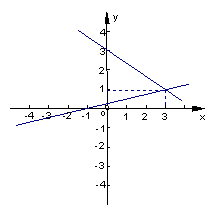
14、如图，直线l1、l2交点坐标可以看作方程组__________的解。
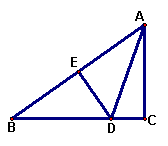
15、如图所示， 在△ABC中，∠C=90°，AB的垂直平分线交BC于点D，如果 ∠CAD=20°，则∠B=_________
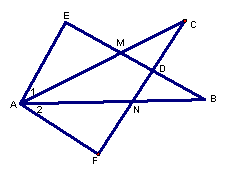
16、如图，∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN。其中正确结论序号是___________________。
17、表中的数据是调查某区中小学生视力情况获得的，请根据表中的数据填空。
| 学段 | 人数 | 视力不良学生人数 | 视力不良率(%) | ||
| 男 | 女 | 合计 | |||
| 小学 | 240 | 23 | 25 | 48 | |
| 初中 | 120 | 28 | 30 | 58 | |
| 高中 | 120 | 41 | 42 | 85 | |
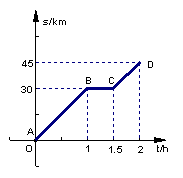18、某人从甲地出发，骑摩托车去乙地，途中因车出现故障而停车修理，到达乙地时正好用了2h，已知摩托车行驶的路程s(km)与行驶时间t(h)之间的函数关系由如图的图象ABCD给出。若这辆摩托车平均每行驶100km的耗油量为2L，根据图中给出的信息，从甲地到乙地，这辆摩托车共耗油_________L。
三、解答题(共66分)
19、（8分）（1）计算(2a+3b-c)(2a-3b+c)
(2)化简求值：(a+2)2-2(a+3)(a-2)+(a-3)2，其中a=-0.75
20、（8分）计算
（1）1213÷（310·411） （2） [6xy2(x2-3xy)-(-3x2y)3]3x2y2
21、（8分）因式分解：
(1) 121(a-b)2-169(a+b)2 (2) a(n-1)2-2a(n-1)+a
22、（8分）求证：如果两个三角形的两个角和其中一个角的平分线对应相等，那么这两个三角形全等。
23、（8分）如图，已知AD是△ABC的角平分线，DE、DF分别是△ABD、△ACD的高。求证：AD垂直平分EF。
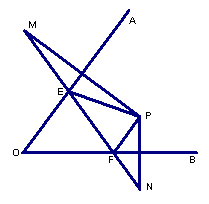
24、（8分）如图，已知点P在∠AOB内，点M、N分别是点P关于直线AO、BO的对称点，M、N的连线与OA、OB交于E、F，若△PEF的周长是20cm。求线段MN的长
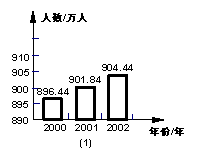
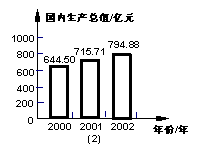25、（8分）先阅读右面两个图表（图1、图2），再解答提出的问题。
（1）请计算出近三年来台州市人均国内生产总值（精确到1元），填入下表：
| 年份（年） | 2000 | 2001 | 2002 |
| 人均国内生产总值（元） |
（2）从2000年到2002年，人均国内生产总值平均每年增长的百分率是多少（精确到0.1%）？
26、（10分）农机租赁公司共有50台收割机，其中甲型20台，乙型30台，现将这50台收割机派往A、B两地，其中30台派往A地，20台派往B地。两地与该农机租赁公司商定的每天的租赁价格见下表：
| 每台甲型收割机的租金 | 每台乙型收割机的租金 | |
| A地 | 1800元 | 1600元 |
| B地 | 1600元 | 1200元 |
（1）设派往A地x台乙型收割机，这50台收割机一天获得的租金为y元，求y与x间的函数关系式，并写出x的取值范围；
（2）若使这50台收割机一天获得的租金总额不低于79600元，说明有多少种分配方案，并将各种方案设计出来；
（3）若要使这50台收割机每天获得的租金最高，请你为公司提一条合理化建议。