第十二讲 平行四边形
平行四边形是一种极重要的几何图形．这不仅是因为它是研究更特殊的平行四边形——矩形、菱形、正方形的基础，还因为由它的定义知它可以分解为一些全等的三角形，并且包含着有关平行线的许多性质，因此，它在几何图形的研究上有着广泛的应用．
由平行四边形的定义决定了它有以下几个基本性质：
(1)平行四边形对角相等；
(2)平行四边形对边相等；
(3)平行四边形对角线互相平分．
除了定义以外，平行四边形还有以下几种判定方法：
(1)两组对角分别相等的四边形是平行四边形；
(2)两组对边分别相等的四边形是平行四边形；
(3)对角线互相平分的四边形是平行四边形；
(4)一组对边平行且相等的四边形是平行四边形．
例1 如图2-32所示．在
ABCD中，AE⊥BC，CF⊥AD，DN=BM．求证：EF与MN互相平分．
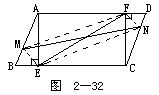
分析 只要证明ENFM是平行四边形即可，由已知，提供的等量要素很多，可从全等三角形下手．
证 因为ABCD是平行四边形，所以
AD
BC，ABCD，∠B=∠D．
又AE⊥BC，CF⊥AD，所以AECF是矩形，从而
AE=CF．
所以
Rt△ABE≌Rt△CDF(HL，或AAS)，BE=DF．又由已知BM=DN，所以
△BEM≌△DFN(SAS)，
ME=NF． ①
又因为AF=CE，AM=CN，∠MAF=∠NCE，所以
△MAF≌△NCE(SAS)，
所以 MF=NF． ②
由①，②，四边形ENFM是平行四边形，从而对角线EF与MN互相平分．
例2 如图2-33所示．Rt△ABC中，∠BAC=90°，AD⊥BC于D，BG平分∠ABC，EF∥BC且交AC于F．求证：AE=CF．
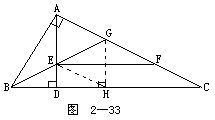
分析 AE与CF分处于不同的位置，必须通过添加辅助线使两者发生联系．若作GH⊥BC于H，由于BG是∠ABC的平分线，故AG=GH，易知△ABG≌△HBG．又连接EH，可证△ABE≌△HBE，从而AE=HE．这样，将AE“转移”到EH位置．设法证明EHCF为平行四边形，问题即可获解．
证 作GH⊥BC于H，连接EH．因为BG是∠ABH的平分线，GA⊥BA，所以GA=GH，从而
△ABG≌△HBG(AAS)，
所以 AB=HB． ①
在△ABE及△HBE中，
∠ABE=∠CBE，BE=BE，
所以 △ABE≌△HBE(SAS)，
所以 AE=EH，∠BEA=∠BEH．
下面证明四边形EHCF是平行四边形．
因为AD∥GH，所以
∠AEG=∠BGH(内错角相等)． ②
又∠AEG=∠GEH(因为∠BEA=∠BEH，等角的补角相等)，∠AGB=∠BGH(全等三角形对应角相等)，所以
∠AGB=∠GEH．
从而
EH∥AC(内错角相等，两直线平行)．
由已知EF∥HC，所以EHCF是平行四边形，所以
FC=EH=AE．
说明 本题添加辅助线GH⊥BC的想法是由BG为∠ABC的平分线的信息萌生的(角平分线上的点到角的两边距离相等)，从而构造出全等三角形ABG与△HBG．继而发现△ABE≌△HBE，完成了AE的位置到HE位置的过渡．这样，证明EHCF是平行四边形就是顺理成章的了．
人们在学习中，经过刻苦钻研，形成有用的经验，这对我们探索新的问题是十分有益的．
例3 如图2-34所示．ABCD中，DE⊥AB于E，BM=MC=DC．求证：∠EMC=3∠BEM．
分析 由于∠EMC是△BEM的外角，因此∠EMC=∠B+∠BEM．从而，应该有∠B=2∠BEM，这个论断在△BEM内很难发现，因此，应设法通过添加辅助线的办法，将这两个角转移到新的位置加以解决．利用平行四边形及M为BC中点的条件，延长EM与DC延长线交于F，这样∠B=∠MCF及∠BEM=∠F，因此， 只要证明∠MCF=2∠F即可．不难发现，△EDF为直角三角形(∠EDF=90°)及M为斜边中点，我们的证明可从这里展开．
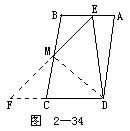
证 延长EM交DC的延长线于F，连接DM．由于CM=BM，∠F=∠BEM，∠MCF=∠B，所以
△MCF≌△MBE(AAS)，
所以M是EF的中点．由于AB∥CD及DE⊥AB，所以，DE⊥FD，三角形DEF是直角三角形，DM为斜边的中线，由直角三角形斜边中线的性质知
∠F=∠MDC，
又由已知MC=CD，所以
∠MDC=∠CMD，
则
∠MCF=∠MDC+∠CMD=2∠F．
从而
∠EMC=∠F+∠MCF=3∠F=3∠BEM．
例4 如图2-35所示．矩形ABCD中，CE⊥BD于E，AF平分∠BAD交EC延长线于F．求证：CA=CF．
分析 只要证明△CAF是等腰三角形，即∠CAF=∠CFA即可．由于∠CAF=45°-∠CAD，所以，在添加辅助线时，应设法产生一个与∠CAD相等的角a，使得∠CFA=45°-a．为此，延长DC交AF于H，并设AF与BC交于G，我们不难证明∠FCH=∠CAD．
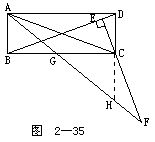
证 延长DC交AF于H，显然∠FCH=∠DCE．又在Rt△BCD中，由于CE⊥BD，故∠DCE=∠DBC．因为矩形对角线相等，所以△DCB≌△CDA，从而∠DBC=∠CAD，因此，
∠FCH=∠CAD． ①
又AG平分∠BAD=90°，所以△ABG是等腰直角三角形，从而易证△HCG也是等腰直角三角形，所以∠CHG=45°．由于∠CHG是△CHF的外角，所以
∠CHG=∠CFH+∠FCH=45°，
所以 ∠CFH=45°-∠FCH． ②
由①，②
∠CFH=45°-∠CAD=∠CAF，
于是在三角形CAF中，有
CA=CF．
例5 设正方形ABCD的边CD的中点为E，F是CE的中点(图2-36)．求证：
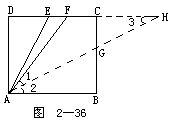
分析 作∠BAF的平分线，将角分为∠1与∠2相等的两部分，设法证明∠DAE=∠1或∠2．
证 如图作∠BAF的平分线AH交DC的延长线于H，则∠1=∠2=∠3，所以
FA=FH．
设正方形边长为a，在Rt△ADF中，
从而
所以 Rt△ABG≌Rt△HCG(AAS)，
从而
Rt△ABG≌Rt△ADE(SAS)，
例6 如图2-37所示．正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G．求证：△GHD是等腰三角形．
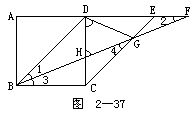
分析 准确地画图可启示我们证明∠GDH=∠GHD．
证 因为DEBC，所以四边形BCED为平行四边形，所以∠1=∠4．又BD=FD，所以
所以 BC=GC=CD．
因此，△DCG为等腰三角形，且顶角∠DCG=45°，所以
又
所以 ∠HDG=∠GHD，
从而GH=GD，即△GHD是等腰三角形．
练习十二
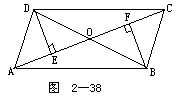
1．如图2-38所示．DE⊥AC，BF⊥AC，DE=BF，∠ADB=∠DBC．求证：四边形ABCD是平行四边形．
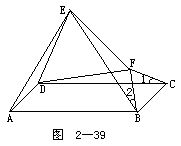
2．如图2-39所示．在平行四边形ABCD中，△ABE和△BCF都是等边三角形．求证：△DEF是等边三角形．
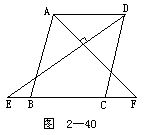
3．如图2-40所示．ABCD中，AF平分∠BAD交BC于F，DE⊥AF交CB于E．求证：BE=CF．
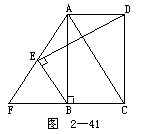
4．如图2-41所示．矩形ABCD中，F在CB延长线上，AE=EF，CF=CA．求证：BE⊥DE．
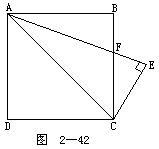
5．如图2-42所示．在正方形ABCD中，CE垂直于∠CAB的平分
