句容市宝华中学第一次月考试卷
（2004～2005学年第一学期）
命题：陈平 审稿：陈平
班级 姓名 得分
一、填空(每空1分，共24分)
1、
的平方根是
；算术平方根是
；-27的立方根是
。
2、在Rt△ABC中, ∠C=90°,AB=15,BC:AC=3:4,BC=___________.
3、满足
的整数y是__________；平方根等于本身的数是__________。
3、计算：（
=
。
4、比较大小 
； 
5、
_____；
_____；
_____；
_____。
6、实数a在数轴上的对应点如上图，则
=
7、若
=9，x= __________。若
=1，x=__________。
8、估算：
=
（误差小于0.1）；
=
（误差小于1 ）
9、若0＜a＜1,a ____
，若a＞1 a ____（填＜、＞、＝）。
10、直角三角形两直角边长分别为6和8，则它斜边上的高为__________。
11、写出三个大于5小于7的无理数 __________。
12、小明把一根90cm长的木棒放到一个长、宽、高分别为50cm、 40cm、 50cm的木箱中，他能放进去吗？答：_______________（填“能”、或“不能”）
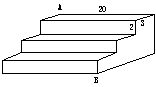13、如图是一个三级台阶，它的每一级的长宽和高分别为25dm、3dm、3dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到 B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是_____________.（结果保留根号）
二、选择题（每题2分，共20分）
1、以下列各组数为边的三角形不是直角三角形的是（ ）
A、24，10，26 B、5，3，4 C、60，11，61 D、5，6，9
2、下列各数中，有理数的个数为（ ）
；
；
；
；0；
；
；
；
；
A、3 B、4 C、5 D、6
3、下列说法中不正确的是（ ）
A、－1的立方根是－1。 B、0的平方根与立方根相等。
C、－4的平方根是
。 D、每个数都有一个立方根。
4、下列各式估算正确的是（ ）
A、
B、
C、
D、
5、下列各式中正确的是（ ）
A、
B、
C、
D、
6、将直角三角形三边扩大同样的倍数，得到的三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、任意三角形
7、下列说法正确的有（ ）
（1）带根号的数是无理数；（2）无理数是带根号的数；（3）开方开不尽的数都是无理数；（4）无理数都是开方开不尽；（5）无理数是无限小数；（6）无限小数是无理数。
A、2个 B、3个 C、4个 D、5个
19、下列各结论中，正确的是（ ）
A、-
= - 6
B、（-
）
=9
C、
±16 D、-（-
）=
20．一个三角形三边的长分别为15cm，20cm，25cm，这个三角形最长边上的高是 [ ]
三、（1）化简（4×4=16分）
1、（
-
）×
2、
-4
3、12
- 6
- 
4、（ - 
）2
（2）求x的值（4×2=8分）
1、
2、4
四、“印度荷花问题”（4分）
¨ 湖静浪平六月天
¨ 荷花半尺出水面
¨ 忽来一阵狂风急
¨ 湖面之上不复见
¨ 入秋渔翁始发现
¨ 残花离根二尺遥
¨ 试问水深有几许？
¨ ——印度数学家拜斯迦罗（公元1114——1185年）
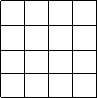五、（6分）如图，正方形网格中的每个小正方形边长都是1，任意连结这些小正方形的顶点，可得到一些线段。请在图中画出
这样的线段，并选择其中的一个说明这样画的道理。
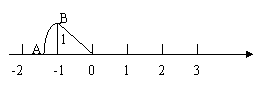六、如图，OA=OB，（8分）
（1）写出数轴上点A表示的数；
（2）比较点A表示的数与－1.5 的大小；
3）这种研究和解决问题的方式，体现了 的数学思想方法。（将下列符合的选项序号填在横线上）
A、数形结合 B、代入 C、换元 D、归纳
（3）在数轴上作出
所对应的点。
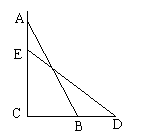
七、（7分）如图，一个梯子AB长2.5 米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.5米，求梯子顶端A下落了多少米？
八、阅读下列短文，回答有关问题：（7分）
在实数这章中，遇到过、
这样的式子，我们把这样的式子叫做二次根式，根号下的数叫做被开方数。如果一个二次根式的被开方数中有的因数能开的尽方，可以利用
将这些因数开出来，从而将二次根式化简。当一个二次根式的被开方数中不含开得尽方的因数或者被开方数中不含有分数时，这样的二次根式叫做最简二次根式，例如，
化成最简二次根式是
，化成最简二次根式是
。几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式叫做同类二次根式，如上面的例子就是同类二次根式。
（1）请判断下列各式中，哪些是同类二次根式？
（2）二次根式中的同类二次根式可以像整式中的同类项一样合并，请计算：
=
）
（