第三章练习
 1.
一顶简易的圆锥形帐篷,帐篷收起来时伞面的长度有4米,撑开后帐篷高2米,则帐篷撑好后的底面直径是 。
1.
一顶简易的圆锥形帐篷,帐篷收起来时伞面的长度有4米,撑开后帐篷高2米,则帐篷撑好后的底面直径是 。
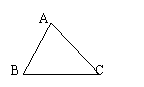
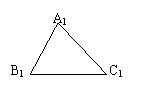
2. △![]() 是△
是△![]() 平移后得到的三角形,则
平移后得到的三角形,则
|
 3从8:55到9:15,钟表的分针转动的角度是 ,时针转动的角度是 。
3从8:55到9:15,钟表的分针转动的角度是 ,时针转动的角度是 。
 4如图(1),以左边图案的中心为旋转中心,将
4如图(1),以左边图案的中心为旋转中心,将
图案按 方向旋转 即可得到左边图案。
5图(2)绕着中心最小旋转 能与自身重合。
 6.从8:45到9:15,钟表的分针转动的角度是 ,时针转动的角度是 。
6.从8:45到9:15,钟表的分针转动的角度是 ,时针转动的角度是 。
7.将任意一个三角形绕着其中一边的中点旋转![]() ,
,
所得图形与原图形可拼成一个 。
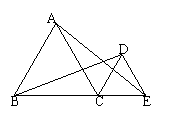
8,△ABC和△DCE是等边三角形,则在此图中,△ACE
绕着 点 旋转 度可得到△ 。
二 选择
(1)下列说法正确的是 。
A. 平移和旋转不改变图形的形状和大小。
B. 平行四边形既是中心对称图形,又是轴对称图形。
C. 任意多边形都可以进行密铺。
D. 对角线互相垂直平分的四边形是正方形。
(2)下列图形中,绕某个点旋转![]() 能与自身重合的有( )
能与自身重合的有( )
①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形
A. 5个 B. 2个 C. 3个 D. 4个
3)某工厂10名工人生产同一种零件,生产的件数分别是15,17,14,10,
15, 17, 17, 16, 14, 12,设其平均数为![]() ,中位数为
,中位数为![]() ,众数
,众数
为![]() ,则有 。
,则有 。
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
三、作图题:(共8分)
(1)将左图绕O点逆时针旋转![]() ,将右图向右平移5格。
,将右图向右平移5格。

![]()
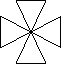 四、利用平移、旋转、轴对称分析下面两个图案的形成过程。(各用两种方法)(6分)
四、利用平移、旋转、轴对称分析下面两个图案的形成过程。(各用两种方法)(6分)
五、利用平移、旋转、轴对称分析下面两个图案的形成过程。(各用两种方法


六、作图题:(共6分)
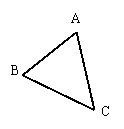 (1)如图,△ABC经过平移后,B点
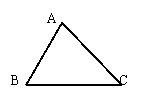
(2)如图,△ABC绕点旋转后,C点移到了C处,作出平移后的三角形。 转到了D处,作出旋转后的三角形。
(1)如图,△ABC经过平移后,B点
(2)如图,△ABC绕点旋转后,C点移到了C处,作出平移后的三角形。 转到了D处,作出旋转后的三角形。
 | |||
| |||
|
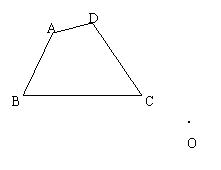 |
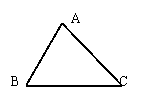
3、将△![]() 平移后,A点移到A1点,请作出平移后的图形,并将此图形绕点C1逆时针旋转
平移后,A点移到A1点,请作出平移后的图形,并将此图形绕点C1逆时针旋转![]() ,再作出所得图形。
,再作出所得图形。
 |
| |||
七.在一次射击比赛中,19名参赛队员(每人打3发)的成绩如下表:
| 成绩(环) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数 | 1 | 1 | 2 | 2 | 4 | 7 | 2 |
(1) 求出这组数据的平均数,众数,中位数。
(2) 在此问题中,平均数,众数,中位数各说明了什么?
第五章练习
一 填空
1)点A在![]() 轴上,距离原点4个单位长度,则A点的坐标是 。
轴上,距离原点4个单位长度,则A点的坐标是 。
 (2)矩形ABCD中,A、B、C三点的坐标分别是(0,0)(6,0)(6,4)则D点的坐标是 ,D点关于
(2)矩形ABCD中,A、B、C三点的坐标分别是(0,0)(6,0)(6,4)则D点的坐标是 ,D点关于![]() 轴的对称点是 。
轴的对称点是 。
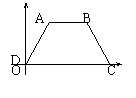
(3)如图,以等腰梯形ABCD的顶点D为原点建立直角
坐标系,若AB=4,CD=10,AD=5,则图中各顶点的
坐标分别是A ,B ,C ,D 。
(4)点A在![]() 轴右侧,距
轴右侧,距![]() 轴4个单位长度,距
轴4个单位长度,距![]() 轴3个单位长度,则A点的坐标是 ,A点离开原点的距离是
。
轴3个单位长度,则A点的坐标是 ,A点离开原点的距离是
。
 (5)点A(
(5)点A(![]() ,5),B(
,5),B(![]() ,
, ![]() )关于
)关于![]() 轴对称,则
轴对称,则![]() 。
。
6)在x轴上与点(0,-2)距离是4个单位长度的点有 。
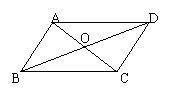
7 如图,正方形OABC的各顶点A、B、C的坐标如图,
则点A、B、C分别关于x轴,y轴,原点的坐标分别
是 , , 。
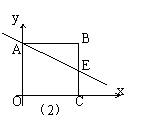 (6)如图(2),正方形ABCO的边长是2,E是BC中点,则E点的坐标是 ,直线AE的解析式是
。
(6)如图(2),正方形ABCO的边长是2,E是BC中点,则E点的坐标是 ,直线AE的解析式是
。
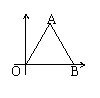 (10)如图,△AOB是边长为5的等边三角形,则A,B两点的坐
(10)如图,△AOB是边长为5的等边三角形,则A,B两点的坐
标分别是A ,B
二选择
1. 如图,右边坐标系中四边形的面积是( )
A. 4 B. 5.5 C. 4.5 D.5
2. 点P(![]() )关于x轴对称与关于y轴对称的点的坐标相同,则
)关于x轴对称与关于y轴对称的点的坐标相同,则![]() 的值分别是 。
的值分别是 。
A. –1, 2 B. –1, –2 C . –2, 1 D. 1, 2
3)将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘以-1,所得图形与原图形的关系是 。
A.关于![]() 轴对称 B.关于
轴对称 B.关于![]() 轴对称 C.关于原点对称 D.无法确定
轴对称 C.关于原点对称 D.无法确定
 |
三 建立坐标系表示右面图形各顶点的坐标
直角梯形上底3,下底5,底角![]()
![]()
![]()
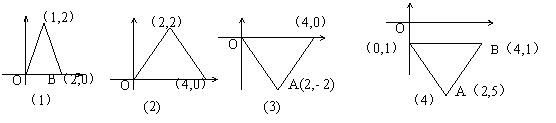
![]() 七、观察图形由(1) (2) (3) (4)的变化过程,写出每一步图形是如何变化的,图形中各顶点的坐标是如何变化的。(6分)
七、观察图形由(1) (2) (3) (4)的变化过程,写出每一步图形是如何变化的,图形中各顶点的坐标是如何变化的。(6分)
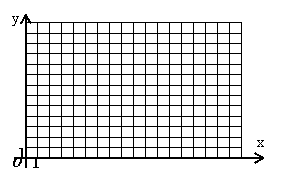 五、作图分析题:(每小题2分,共10分)
五、作图分析题:(每小题2分,共10分)
(1) 在如图直角坐标系中,描出点(9,1)
(11,6)(16,8)(11,10)(9,15)
(7,10)(2,8)(7,6)(9,1),
并将各点用线段顺次连接起来。
(2) 这个图形是中心对称图形吗?如果是,它的对称中心的坐标是什么?
(3) 将上面各点的横坐标不变,纵坐标缩小为原来的一半,求出各点的坐标,再将各点依次连接起来。与原图形相比,所得图形有什么变化?
(4) 如果将原图形上各点的横坐标加2、纵坐标减5,猜一猜,图形会发生怎样的变化?
(5)
如果想让变化后的图形与原图形关于原点对称,原图形各点的坐标应该如何变化?
2、建立坐标系表示下列图形各顶点的坐标:(12分)
(1)菱形ABCD,边长3,![]() (2)长方形ABCD,长6宽4,建坐标系
(2)长方形ABCD,长6宽4,建坐标系
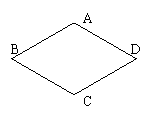 使其中C点的坐标(-3,2)
使其中C点的坐标(-3,2)

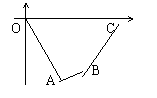
3、在图中A(2,-4)B(4,-3)C(5,0),求四边形ABCO的面积。(6分)
八年级数学摸底检测二
一、 填空题(每空2分,共40分)
1. 在![]() ,3.33,
,3.33,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() 中,有理数有
,无理数有
,
中,有理数有
,无理数有
,
正数有 ,负数有 。
2.
121的算术平方根的平方根是 ,![]() = 。
= 。
3. 从12:00到12:30,分针转了 度,时针转了 度。
![]() 4. ABCD中,
4. ABCD中,![]() ,则
,则![]() ,
,![]() =
。
=
。
5. 菱形的两条对角线长分别是16cm和12cm,则菱形的边长是 ,高 ,面积是 。
 6. 如图,正方形OABC的各顶点A、B、C的坐标如图,
6. 如图,正方形OABC的各顶点A、B、C的坐标如图,
则点A、B、C分别关于x轴,y轴,原点的坐标分别
是 , , 。
7.已知点A(![]() ,
,![]() )在函数
)在函数![]() 的图像上,则
的图像上,则![]() = 。
= 。
![]() 8. 若 x=2是方程2x+3my=1的一个解,则m= 。
8. 若 x=2是方程2x+3my=1的一个解,则m= 。
y=1
9. 一个射手连续打靶20次,其中2次射中10环,7次射中9环,8次射中8环,3次射中7环,这个射手每次射中环数的众数是 ,中位数是 。
二、
![]()
![]() 化简计算:(每小题4分,共24分)
化简计算:(每小题4分,共24分)
(1) ![]() (2)
(2) ![]()
![]()
![]()
![]() (3)
(3) ![]() (4)
(4)![]()
![]()
(5)![]() (6)
(6)![]() -
-![]()
三、
|
 |
四、
在矩形ABCD中,两条对角线AC、BD相交于O,![]() ,AB=4
,AB=4
①
 判断△AOB的形状;
判断△AOB的形状;
②  求对角线AC、BD的长。(8分)
求对角线AC、BD的长。(8分)
五、 列方程组解应用题:(7×2=14分)
1.A、B两地相距36千米,甲从A地、乙从B地同时出发,相向而行,2小时相遇后,甲再走2小时30分钟到达B地,乙再走1小时36分钟到达A地,求两人的速度。
2.某工厂两个车间去年计划共完成利税720万元,结果甲车间完成了计划的115%,乙车间完成了计划的110%,结果两车间共完成利税812万元,求这两个车间实际各完成利税多少万元?
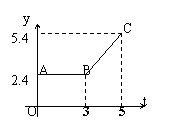 六、图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图像。
六、图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图像。
① 从图像知,通话2分钟需付的电话费是 元。
② 当t≥3时求出该图像的解析式(写出求解过程)。
通话7分钟需付的电
八年级上学期数学摸底检测一
六、 填空题(每空2分,共36分)
1. 48的平方根是 ,![]() 的立方根是 。
的立方根是 。
2. 一顶简易的圆锥形帐篷,帐篷收起来时伞面的长度有4米,撑开后帐篷高2米,则帐篷撑好后的底面直径是 。
 3. 从12:40到13:10,钟表的分针转动的角度是 ,时针转动的角度是 。
3. 从12:40到13:10,钟表的分针转动的角度是 ,时针转动的角度是 。
![]() 4. 在 ABCD中,
4. 在 ABCD中,![]() ,
,![]() ,BC=2AB
,BC=2AB
![]() 则AC= ,BD= , ABCD的面积是 。
则AC= ,BD= , ABCD的面积是 。
5. 在菱形ABCD中,AB=AC=10,则∠A= ,BD= 。
6. 等腰梯形高4㎝,上底4㎝,下底6㎝,则对角线长 。
7. 点A(![]() ,
,![]() ),B(
),B(![]() ,
, ![]() )关于
)关于![]() 轴对称,则
轴对称,则![]() = ,b= 。
= ,b= 。
8. 水池中原有水100立方米,现在以每分钟16立方米的速度向水池中注水,则水池中的总水量V(立方米)与注水时间t(分钟)之间的关系 。
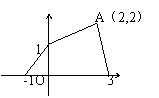
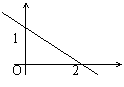 9. 如图,一次函数图像如图所示,则函数关系式是 。
9. 如图,一次函数图像如图所示,则函数关系式是 。
10. 某班一次体育测试中得100分的有4人,90分的有11人,
80分的有11人,70分的有8人,60分的有5人,剩下8人
一共得了300分,则平均数是 (精确到0.1),众数是 ,
中位数是
七、 选择题:(每小题3分,共24分)
1. 下列说法正确的有( )
①无理数是无限小数;②无限小数是无理数;③开方开不尽的数是无理数;
④两个无理数的和一定是无理数;⑤无理数的平方一定是有理数;
A.1个 B.2个 C.3个 D.4个
2. 用下列两种图形不能进行密铺的是( )
A.三角形,平行四边形 B.正方形,正八边形
 C.正六边形,正三角形
D.正六边形,正八边形
C.正六边形,正三角形
D.正六边形,正八边形
3. 如图,右边坐标系中四边形的面积是( )
A. 4 B. 5.5 C. 4.5 D.5
4. 四边形ABCD中,AC、BD交于点O,则下列条件
能判断四边形是正方形的有 。
① AC⊥BD,AO=CO=BO=DO ②AB=CD=AD=BC,AC=BD ③AO=BO=CO=DO
④![]() ⑤AB∥CD,AB=BC=CD
⑤AB∥CD,AB=BC=CD
A. 2个 B. 3个 C.4个 D.5个
5. 下面哪个点不在函数![]() 的图像上(
)
的图像上(
)
A.(-5,13) B.(0.5,2) C(3,0) D(1,1)
6. 在函数![]() 中,y随x的增大而增大,则k的值可能是( )
中,y随x的增大而增大,则k的值可能是( )
A.1 B. ![]() C.2 D.
C.2 D. ![]()
7. 下列命题正确的是( )
① 对角线互相垂直且相等的平行四边形是正方形
② 平行四边形、矩形、等边三角形、正方形既是中心对称图形,也是轴对称图形。
③ 旋转和平移都不改变图形的形状和大小
④
底角是![]() 的等腰梯形,高是
的等腰梯形,高是![]() ,则腰长是
,则腰长是![]() 。
。
A. 全对 B. ①②④ C. ①②③ D. ①③④
8. 甲、乙两人练习赛跑,若甲先跑半小时,则乙出发后40分钟可追上甲,设甲、乙每小时分别跑x千米、y千米,则可列方程( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
八、 化简计算:(每小题3分,共18分)
(1)![]() (2)
(2)![]() (3)
(3)![]() +
+![]()
![]()
![]()
![]() (4)
(4) ![]() (5)
(5) ![]() (6)
(6)![]()
![]()
![]()
![]()
 |
九、
|
(2)如图,在方格直中建立直角坐标系,画出一次函数
y=4-2x的图像
十、 解答题:
(1)计算下列各式并观察:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,
,
通过上述各式,你能发现什么样的规律,用自己的语言叙述出来
。
(2)建立坐标系表示右面图形各顶点的坐标
 直角梯形上底3,下底5,底角
直角梯形上底3,下底5,底角![]()
(3)上个月,商店共卖出甲、乙两种商品1000件,这个月甲商品多卖出50%,乙商品少卖出10%,结果产品的总销量减少了4%,上个月甲、乙两种商品各卖出多少件?
 (4)A、B两地相距36千米,甲乙两人同时从A、B两地出发相向而行,4小时相遇;若走6小时,甲所余路程是乙所余路程的两倍,求甲、乙速度。
(4)A、B两地相距36千米,甲乙两人同时从A、B两地出发相向而行,4小时相遇;若走6小时,甲所余路程是乙所余路程的两倍,求甲、乙速度。
 |
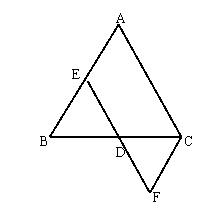
(5)已知:如图,在△ABC中,AB=AC,E是AB中点,
以E为圆心,EB为半径画弧交BC于D点,
连接ED并延长到F,使DF=DE
求证:![]()
(6)汽车在行驶时,由于惯性作用,刹车后还要向前滑行一段距离才会停止,我们称这段距离为“刹车距离”。现在甲乙两车在一个弯道上相向而行,在相距16米的地方发现情况不对,同时刹车。根据有关资料,甲、乙两车刹车距离S(米)与车速v(千米/时)之间与如下关系:
①
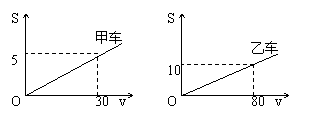 分别求出两个函数的关系式
分别求出两个函数的关系式
② 若甲、乙两车的速度都是60千米/时,两车是否相撞?说说你的理由。
(7)某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,如超计划用水,则每吨按0.8元收费。如单位自建水泵房抽水,每月需500元管理费,然后每用一吨水的费用为0.28元。已知每抽一吨水需成本0.07元。
① 写出若该单位用自来水公司的水及自建水泵时水费y(元)与用水量(吨)的关系。
② 若该单位用水3100吨,是用自来水公司水合算,还是自建水泵房抽水合算?
2003—2004学年度第一学期期末初二数学试题
考试时间(90分钟)满分120分
十一、 填空题(每空2分,共30分)
 1.
1. ![]() ,
,![]() 的算术平方根的平方根是 。
的算术平方根的平方根是 。
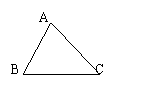
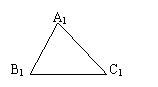
2. △![]() 是△
是△![]() 平移后得到的三角形,则
平移后得到的三角形,则
|
3. 菱形有一个内角是![]() ,边长为10,则它的面积是 。
,边长为10,则它的面积是 。
4. 正方形的对角线 、 、 ,且每一条对角线平分一组对角。
 5. 三角形的三条中线交于一点,这个点是三角形的 。
5. 三角形的三条中线交于一点,这个点是三角形的 。
6.
如图,等腰梯形ABCD中,![]() ,AB=4,CD=10,则各顶
,AB=4,CD=10,则各顶
点的坐标是A(7,0) B ,C , D(0,0)。
7. y吨货物用x辆卡车去装,每车装7吨,还有3吨没装上,可列
出方程 ,其中y是否可以看作x的函数(填是或否) 。
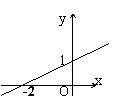 8. 如图所示,图中函数的解析示为
。
8. 如图所示,图中函数的解析示为
。
9. 一次函数y=-2x+b与x轴交于(4,0),则它与y轴的交
点为 ,与直线y=x的交点坐标为 。
二、选择题(每小题3分,共18分)
1. 下列说法正确的有 个。
① 任何正数的两个平方根的和等于0 ② 任何实数都有一个立方根
③ 无限小数都是无理数 ④ 实数和数轴上的点一一对应
A. 1 B. 2 C. 3 D. 4
2. 矩形ABCD的对角线AC,BD所成的锐角是60度,则 。
A. AC+BD=AB+BC+CD+DA B. BD+AC=AB+AC C.BD=2AB D.以上都不对
3. 一个多边形的每个内角都等于![]() ,则内角和是 ,共有 条对角线。
,则内角和是 ,共有 条对角线。
A. ![]() , 8
B.
, 8
B. ![]() , 10 C.
, 10 C. ![]() , 9
D.
, 9
D. ![]() , 11
, 11
4. 下列表述的图形中能进行密铺的有 种。
① 平行四边形 ② 三角形 ③直角梯形 ④正五边形 ⑤正八边形
A. 1 B. 2 C. 3 D. 4
5. 方程2x+y=7在自然数范围内的解有 对。
A. 4 B. 3 C. 2 D. 1
6. 点P(![]() )关于x轴对称与关于y轴对称的点的坐标相同,则
)关于x轴对称与关于y轴对称的点的坐标相同,则![]() 的值分别是 。
的值分别是 。
A. –1, 2 B. –1, –2 C . –2, 1 D. 1, 2
三、 解答题:
3、作图题:(6分)将△![]() 平移后,A点移到A1点,请作出平移后的图形,并将此图形绕点C1逆时针旋转
平移后,A点移到A1点,请作出平移后的图形,并将此图形绕点C1逆时针旋转![]() ,再作出所得图形。
,再作出所得图形。
 |
| |||
1.化简二次根式:(每小题3分,共9分)
(1)![]() (2)
(2)![]() (3)
(3)![]()
 |
4、(8分)如图,菱形ABCD中,E是AD中点,
EF⊥AC交CB的延长线与点F。
(1) DE和BF相等吗?请说明理由。
(2) 连结AF、BE,四边形AFBE是平
行四边形吗?说明理由。
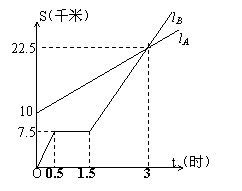 5、(16分)如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
5、(16分)如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1)B出发时与A相距 千米。(2分)
(2)走了一段路后,自行车发生故障,进行
修理,所用的时间是 小时。(2分)
(3)B出发后 小时与A相遇。(2分)
(4)若B的自行车不发生故障,保持出发时
的速度前进, 小时与A相遇,相遇点
离B的出发点 千米。在图中表示出
这个相遇点C。(6分)
(5)求出A行走的路程S与时间t的函数关系式。(写出过程,4分)
6、(9分)在一次射击比赛中,19名参赛队员(每人打3发)的成绩如下表:
| 成绩(环) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数 | 1 | 1 | 2 | 2 | 4 | 7 | 2 |
(3) 求出这组数据的平均数,众数,中位数。
(4) 在此问题中,平均数,众数,中位数各说明了什么
7、列方程组解应用题:(8分)
甲、乙两种商品原来的单价和为100元,因市场变化,甲商品提价40%,乙商品降价10%,两种商品的单价和比原来提高了20%,甲、乙两种商品原来的单价各是多少元?
8、请你用树状图的方式排列一下本学期数学课本中的主要内容。(5分)写在背面
9、设计题(3分)
![]() 如图,等腰梯形的一条对角线将它分成了两个三角形,用这两个三角形能否进行密铺,如果能,请设计一个密铺图案,如果不能,请说明理由。
如图,等腰梯形的一条对角线将它分成了两个三角形,用这两个三角形能否进行密铺,如果能,请设计一个密铺图案,如果不能,请说明理由。
第二、四章练习
(1)带根号的数一定是无理数( );(2)无理数都是无限小数( );
(3)无理数包含正无理数、0、负无理数( );(4)4的平方根是2( );
(5)无理数一定不能化成分数( ); (6)![]() 是5的平方根( );
是5的平方根( );
(7)一个正数一定有两个平方根( );(8)![]() 25的平方根是
25的平方根是![]() ( )
( )
(9)互为相反数的两数的立方根也互为相反数( );
(10)负数的平方根、立方根都是负数( );
(11)①无理数是无限小数;②无限小数是无理数;③开方开不尽的数是无理数;
④两个无理数的和是无理数;⑤无理数的平方一定是有理数;
(12)把下列各数填入相应的集合中(只填序号):
①![]() ②
②![]() ③
③![]() ④
④![]() ⑤0 ⑥
⑤0 ⑥![]() ⑦
⑦![]() ⑧
⑧![]()
有理数集合:{ …}
无理数集合:{ …}正数集合{ …}
(13)把下列各数填入相应的集合中(只填序号):
①3.14 ②![]() ③
③![]() ④
④![]() ⑤0 ⑥
⑤0 ⑥![]() ⑦
⑦![]() ⑧0.15
⑧0.15
有理数集合:{ …}正数集合{ …}
无理数集合:{ …}负数集合{ …}
(14)36的算术平方根是 ,1.44的平方根是 ,11的平方根是 ,
的平方根是![]() ,
,![]() 的算术平方根是 ,
的算术平方根是 ,![]() 是 的平方
是 的平方
![]() 15)在 ABCD中,
15)在 ABCD中,![]() ,则
,则![]() 。
。
![]() (16) ABCD周长30㎝,AB:BC=3:2,则AB= ,BC= 。
(16) ABCD周长30㎝,AB:BC=3:2,则AB= ,BC= 。
(15)
![]() ABCD中,对角线BD、AC相交与O,且BD⊥AB,若CD=4㎝,
ABCD中,对角线BD、AC相交与O,且BD⊥AB,若CD=4㎝,
AO=5㎝,则AB= ,BD= , ABCD的面积是 。
二
(1)对角线互相垂直且相等的四边形一定是 。
E. 正方形 B. 矩形 C. 菱形 D. 以上都不是
(2)下列说法正确的是 。
A. 四条边都相等的四边形是正方形B. 四个角都相等的四边形是正方形
C. 对角线相等的菱形是正方形 D.一条对角线平分一组对角的四边形是菱形
(4)下列说法不正确的是 。
A. 两组对角分别相等的四边形是平行四边形 B. 一组邻边都相等的四边形是菱形
C.对角线互相平分的四边形是平行四边形D.两个邻角为直角,对角线相等的矩形是正方形
(5)用两个全等的三角形拼四边形,可拼成 个平行四边形。
A. 3个 B. 2个 C. 5个 D. 4个
(6)平行四边形ABCD中,![]() 的值可能是 。
的值可能是 。
A. 1:2:3:4 B. 1:2:2:1 C. 2:2:1:1 D. 2:1:2:1
① 对角线互相平分的四边形是平行四边形 ② 对角线相等的四边形是矩形
③ 对角线互相垂直的四边形是菱形 ④ 对角线互相垂直且相等的平行四边形是正方形
⑤ 对角线相等的平行四边形是矩形
(7)下列说法正确的有 个。A.1个 B. 2个 C. 3个 D. 5个
①有两个底角相等的梯形是等腰梯形 ②有两边相等的梯形是等腰梯形
③ 有两条对角线相等的梯形是等腰梯形 ④ 等腰梯形上下底中点连线八梯形分成面积相等的两部分 ⑤ 等腰梯形腰是下底的一半,则下底角为![]()
十二、
|
 |