人教实验版八年级(上)数学单元目标检测题（十三）
期末复习（一）
班级 姓名 号次
一、选择题（本题共10题，每题3分，共30分）
1、下列各式分解因式正确的是（ ）
A． 2（m－n）2－6（n－m）3=2（m—n）2（1－3m－3n）
B． －m4－n4=－（m2+n2）（m+n）（m－n）
C．
D．m4－2m2n2+n4=（m+n）2（m－n）2
2、在下列条件下，不能说明⊿ABC≌⊿A/B/C/的是（ ）
A．∠A=∠A/，∠C=∠C/，AC=A/C/
B．∠A=∠A/，AB=A/B/，BC=B/C/
C．∠B=∠B/，∠C=∠C/，AC=A/C/
D．BA=B/A/，BC=B/C/，AC=A/C/
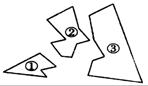3、如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
（A）带①去 （B）带②去（C）带③去 （D）带①和②去
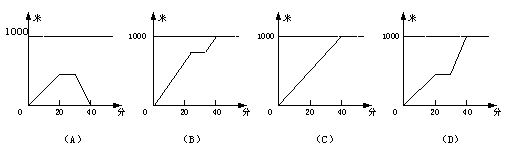
4、小颖从家到学校是1000米，她以不变的速度从家出发20分钟到书店看了10分钟的书，接着她加快步伐匀速行走，用10分钟到了学校，下列图象
中表示小颖从家到学校的时间（分）与路程（米）之间的关系是（ ）
5、下列图案是几种名车的标志，请你指出，在这几个图案中是轴对称图形的共有（ ）
 |
A.1个； B.2个； C. 3个 ； D.4个。
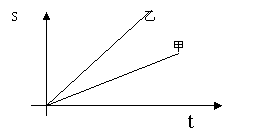6、如图，射线甲、乙分别表示甲、乙两车所走路程
与时间的关系图，则两车速度关系是：( )
A 、 甲比乙快 ； B 、乙比甲快 ；
C 、 甲乙同速 ； D 、不能判断。
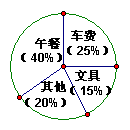
7、小明把自己一周的支出情况，用如图所示的统计图来表示，下面说法正确的是（ ）
A． 从图中可以看出具体的消费数额；
B． 从图中可以直接看出各项消费额占总消费额的百分比；
C． 从图中可以看总消费数额；
D．从图中可以看出各项消费额在一周的具体变化情况。
8、下列计算正确的是（ ）
（A）
（B）
（C）
（D）
9、若
，则x的取值是（ ）
（A）
（B）x≥—
(C) x＞— （D）x≠
10、我们规定这样一种运算：如果
，那么b就叫做以a为底的N的对数，记做
logaN。例如：因为23=8，所以log28=3，那么log381的值为（
）
A．27 B 9 C 4 D 381
二、（本题共8题，每题4分，共32分）
11、请你写出一个二次三项式，使得二次项系数为3，
12、若4x2－kxy+y2表示一个完全平方式，则k=
13、一个等腰三角形的两边长分别为4㎝和6㎝，则它的周长为
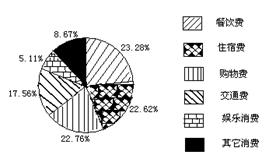14、据2005年5月8日《台州晚报》报道：今年“五一”黄金周期间,我市实现旅游收入再创历史新高,旅游消费呈现多样化,各项消费所占的比例如图秘所示,其中住宿消费为3438.24万元. 则餐饮消费为 万元
15、请写出符合下列性质的一个函数，①图象经过第二象限②y随x 的增大而增大，这个函数可以是
16、观察：1×3+1=22 2×4+1=32
3×5+1=42 4×6+1=52……
请你用一个字母的等式表示你发现的规律：
17、在Rt⊿ABC中，∠C=90°，∠A=30°，AB=12，则BC= 。
18、在实数范围内分解因式：ab2－2a＝_________.
三、解答题
19、（a+2）2—（a+1）（a—1）
20、因式分解 2x2y3－8x4y5
21．如图，在△ＡＢＣ中，点Ｄ在ＡＢ上，点Ｅ在ＢＣ上，ＢＤ＝ＢＥ。
请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。
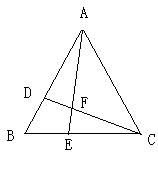你添加的条件是：___________
证明：
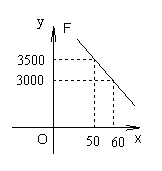
22、近几年，扬州先后获得了“中国优秀旅游城市”和“全国生态建设示范城市”等十多个殊荣。到扬州观光旅游的客人越来越多，某景点每天都吸引大量的游客前来观光。事实表明，如果游客过多，不利于保护珍贵文物，为了实施可持续发展，兼顾社会效益和经济效益，该景点拟采用浮动门票价格的方法来控制游览人数。已知每张门票原价为40元，现设浮动门票为每张
元，经市场调研发现一天游览人数
与票价之间存在着如图所示的一次函数关系。
（1）根据图象，求与之间的函数关系式；
（2）若设
，求该景点一天参观的人数的范围。
23、阅读材料，大数学家高斯在上学读书时
曾经研究过这样一个问题：
1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+
，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…
＝？
观察下面三个特殊的等式
将这三个等式的两边相加，可以得到1×2+2×3+3×4＝
读完这段材料，请你思考后回答：
⑴
⑵
（3）1×2×3×4＋2×3×4×5＋…＋n（n＋1）（n+2）（n+3）=