初二数学上学期第二次测评
时间：90分 满分：100分 姓名
一、填空题（每小题2分，共30分）
1、已知
是完全平方式，则ｍ＝
2、等腰三角形的顶角是120°，底边上的高是3cm，则腰长为______cm．
3、20062 —2005×2007＝
4、
的解为
5、已知△ABC中，AB＝AC，∠A＝2∠B，则∠A＝
6、已知：
，则
，ab=
7、小强调查“每人每天的用水量”这一问题时，收集到80个数据，最大数据是69升，最小数据是42升，若取组距为4，则应分为______组绘制频数分布表．
8、－22006×（－0.5）2008=
9、已知：a2+b2=13，ab=6，则a+b的值是________．
10、等腰三角形是轴对称图形，它的对称轴是
11、函数
中，x的取值范围是
12、函数
的图象上有两点：
且x1<x2，则y1、y2的大小关系是
13、已知正方形的面积为
，则该正方形的边长为
14、分析数据时，为了能清楚地反映事物地变化情况，可以选择________图；为了能清楚地表示出各部分在总体中所占的百分比，通常选用_______图；而为了能表示出每个项目的具体数目，我们又常选用_________图．
15、计算：
＝
二、选择题（每小题3分，共24分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
1、将平面直角坐标系内的△ABC的三个顶点坐标的横坐标乘以-1，纵坐标不变，则所得的三角形与原三角形
A．关于x轴对称 B．关于y轴对称 C．关于原点对称 D．无任何对称关系
2、已知一次函数y=mx+│m+1│的图像与y轴交于点（0，3），且y随x的增大而增大，则m 的值为 A．2 B．—4 C．—2或—4 D．2或—4
3、已知等腰三角形的周长为20cm，将底边长y（cm）表示成腰长x（cm）的函数关系式是y=20-2x，则其自变量x的取值范围是
A．0<x<10 B．5<x<10 C．一切实数 D．x>0
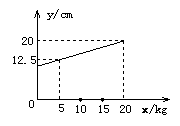
4、弹簧的长度与所挂物体的质量关系为一次函数，由图可
知，不挂物体时，则弹簧的长度为
A．7cm B．8cm C．9cm D．10cm
| 星期天次序 | 1 | 2 | 3 | 4 |
| 搜集电池节数 | 80 | 63 | 51 | 32 |
5、如图所示，在一个月的四个星期天中，某校环保小组共搜集废电池226节，每个星期天所搜集的电池数量如下表：
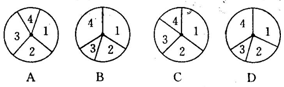下面四幅关于四个星期天搜集废电池节数的统计图中，正确的是
6、已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小，则一次函数y=x＋k的图象大致是
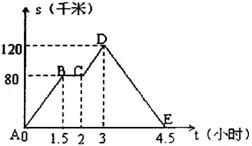
7、如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为60千米／时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．其中正确的说法共有
A.1个 B．2个 C．3个 D．4个
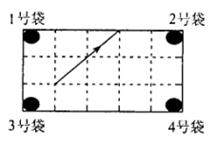
8、如图，是一个台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击中(球可以经过多次反射)，那么该球最后将落入的球袋是
A．1号袋 B．2号袋 C．3号袋 D．4号袋
三、解答题
1、 把下列多项式分解因式（15分）
①
②
③
④
⑤
2、（7分）求证：等腰三角形两腰上的高的交点到底边两端的距离相等．（要求：画出图形，并写出已知、求证、证明）
3、（6分）已知图7中A、B分别表示正方形网格上的两个轴对称图形（阴影部分），其面积分别记为S1、S2（网格中最小的正方形的面积为一个单位面积），请你观察并回答问题．
（1）填空：S1∶S2的值是__________．
（2）请你在图C中的网格上画一个面积为8个平方单位的轴对称图形．
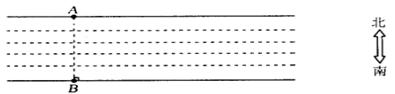4、（6分）一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．(要求，画出示意图，并标出字母，结合图形简要叙述你的方案)
5、（6分）某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：
| 运输工具 | 运输费单价 （元/吨·千米） | 冷藏费单价 （元/吨·小时） | 过路费 （元） | 装卸及管理费 （元） |
| 汽车 | 2 | 5 | 200 | 0 |
| 火车 | 1.8 | 5 | 0 | 1600 |
注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨小时”表示每吨货物每小时的冷藏费．
（1）设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y1（元）和y2（元），试求出y1和y2和与x的函数关系式；
（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？
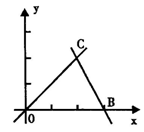
6、（6分）如图，直线OC、BC的函数关系式分别是y1=x和y2=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．
（1）求点C的坐标，并回答当x取何值时y1>y2？
（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．
（3）当x为何值时，直线m平分△COB的面积？