上虞市2005学年第一学期八年级期末考试
数 学 卷
（时间90分钟，满分100分）
| 题号 | 一 | 二 | 三 | 总分 | ||||||
| 1-10 | 11-20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | ||
| 得分 | ||||||||||
| 评卷人 | ||||||||||
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现！
一、选择题（下面各题的备选答案中，只有一个是正确的，将正确答案的序号填在题后的括号内．每小题3分，共30分）
1、下列计算结果为a8的是（ ）
A、a2-a4 B、a4+a4 C、(a4)2 D、2a4
2、在下列四个式子中从左到右的变形，是因式分解的有 （ ）
①
②
③
④
A、4个 B、3个 C、2个 D、1个
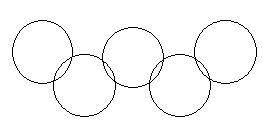3、如图是国际奥林匹克运动会会旗的标志图案，它有五个半径相同的圆组成的，象征着五大洲体育健儿，为发展奥林匹克精神而团结起来，携手拼搏，那么这个图案是（ ）
A、 旋转对称图形 B、 轴对称图形
C、 中心对称图形
D、既是轴对称图形又是中心对称图形
4、小聪同学已经抛掷硬币99次，其中50次为正面，49次为反面，则小聪同学第100次抛掷的结果为（ ）
A．正面 B．反面 C．正面或反面 D．以上都不对
5、根据下图所示，对a、b、c三种物体的质量判断正确的是 ( ）
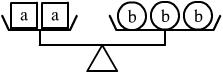
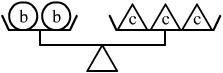
A. a>c B. a<b C. a<c D. b<c
6、在做“抛掷两枚硬币实验”时，有部分同学没有硬币，因而需要选用别的实物来替代进行实验，在以下所选用的替代物中，你认为较合适的是( )
A、两张扑克牌，一张是红桃，另一张是黑桃 B、两个乒乓球，一个是黄色，另一个是白色
C、两个相同的矿泉水瓶盖
D、四张扑克牌，两张是红桃，另两张是黑桃
7、用两块完全一样的含30º的直角三角板，拼下列图形：（1）矩形（2）菱形（3）平行四边形
（4）正方形（5）等腰三角形，一定能拼成的个数有（ ）
A、4 B、3 C、2 D、1
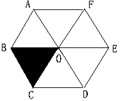
8、如图,O是正六边形ABCDEF的中心, 下列图形中可由ΔOBC平移得到的是 ( )
A. ΔOAF B.ΔOAB C. ΔOCD D.ΔOEF
9、如图，小聪同学拿一张矩形纸图（1），沿虚线对折一次得图（2），又将对角两顶点重合折叠得图（3）．按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是（ ）
A、都是等腰梯形 B、都是等边三角形
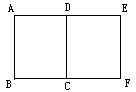C、两个直角三角形，一个等腰三角形 D、两个直角三角形，一个等腰梯形
10、如图，如果正方形ABCD旋转后与正方形CDEF重合，那么图形所在的平面上可以作为旋转中心的点共有（ ）
A、4个 B、3个 C、2个 D、1个
二、填空题（每小题2分，共20分）
11、算一算：
．
12、想一想：
．
13、多项式
是一个完全平方式，则M等于（填一个即可） ．
14、抛掷一枚普通均匀的正方体的骰子，正面出现6的机会约是 .．
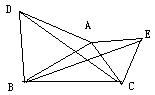
15、如图，在△ABC中，∠BAC=80º，分别以AB、AC为边，作等边△ABD和等边△ACE，连DC、BE，则△ADC绕点A最少旋转 度角后与△ABE重合．
16、菱形的两对角线长分别为4cm，6cm，则菱形的面积为 cm2．
17、在x2□2x□1的空格中，任意填上“+”或“-”，其中能构成完全平方数的机会是
．
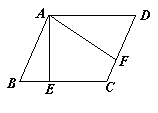
18、、如图，在□ABCD中，AE⊥BC于E，AF⊥CD
于F，∠BAD=120º，则∠EAF=__________．
19、A、B、C、D在同一平面内，从①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD这四个条件中任选两个，能使四边形ABCD是平行四边形的选法有 种．
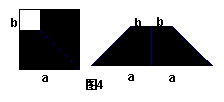20、如图4，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式
．
三、解答题（本大题有7题，共50分）
21、(本题8分)计算下列各题：
（1）( a2 + 3 )( a –2 ) – a (a2 – 2 a – 2 ). （2） (x＋3)2－(x＋2)(x－2)
22、(本题8分)把下列多项式分解因式：
（1）12x5－3x3 (2) (x2＋y2)2－4x2y2
23、(本题6分) 有一种彩票， 投注规则如下：你可以从000~999中任意选取一个整数作为一注投注号码进行投注，中奖号码是位于000~999之间的一个整数，若你所选号码与中奖号码相同即可获奖．
（1）你能预测中奖的机会是多少吗？
(2) 中奖号码中有三个相同数字的机会有多大？三个数字不全相同的机会有多大？
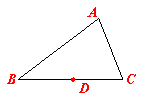24、(本题6分) 如图，在△ABC中，已知D为BC边的中点．
(1)将△ABC绕着点D旋转180º，画出旋转后的△EBC．
(2)四边形ABEC是怎样的四边形？请说明你的理由．
25、（本题6分）解不等式组, 并把解集在数轴上表示出来．再写出它的整数解．
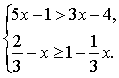
26、（本题8分）某公司为了扩大经营，决定购进6台机器用于生产某种活塞,现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示，经过预算，本次购买机器所耗资金不能超过36万元．
（1）按该公司要求可以有几种购买方案？
（2）若该公司购进的6台机器的日生产力不能低于420个，那么为了节约资金应选择哪种购买方案？
| 甲 | 乙 | |
| 价格（万元/台） | 7 | 5 |
| 每台日生产量（个） | 100 | 60 |
27、（本题8分）
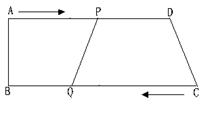
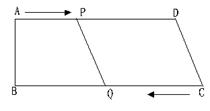
如图，在直角梯形ABCD中，AD∥BC，∠B=900，AB=8厘米，AD=24厘米，BC=26厘米，点P从点A开始沿AD边向点D以1厘米/秒的速度移动，点Q从点C开始沿CB边向点B以3厘米/秒的速度移动.如果点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止移动.设移动的时间为t秒.
求：（1）当t为何值时，四边形PQCD为平行四边形？
（2）当t为何值时，四边形PQCD为等腰梯形？此时梯形PQCD的面积为多少？
参考答案
一、选择题：1-5题C D B C A 6-10题 D B A C B
二、填空题：11、
， 12、
， 13、
， 14、
， 15、60º，
16、12， 17、
， 18、60º 19、4， 20、
三、解答题
21、（1）原式=
（2分） =5a-6 （2分）
（2）原式=
（2分） =6x+13 （2分）
22、（1）原式=12x5－3x3 = 3x3(4x2－1) （2分）=3x3(2x－1)(2x＋1) （2分）
（2）原式=(x2＋y2)2－4x2y2=(x2＋y2－2xy)(x2＋y2+2xy) （2分）= (x－y) 2(x＋y) 2（2分）
23、解：(1) 
(2) 
， 
24、(1) 正确画出旋转后的△EBC．……(2分)
(2) 理由为：四边形ABEC是平行四边形………(3分)
因为D为BC中点，所以BD=DC………(4分)
又因为△ABC和△EBC关于点D中心对称， 所以AD=DE………(5分)
所以四边形ABEC是平行四边形………(6分)
25、分别解两个一元一次不等式得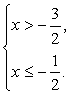
(2分)，解集为
＜
(３分)
把解集在数轴上表示出来(5分)．再写出它的整数解
．(6分)
26、设购买甲种机器x台，则乙种机器为（6-x）台．
（1） 由题意得 7x+5(6-x)≦36 解得x≦3
∵x取值为自然数，∴x=0或1或2 或3 (2分)
即有四种购买方案：甲种机器不买，乙种机器买6台；甲种机器买1台，乙种机器买5台；甲种机器买2台，乙种机器买4台；甲种机器买3台，乙种机器买3台．(4分)
（2）由题意得100x+60(6-x)≧420
解得x≧1.5,从（1）知：1.5≦x≦3，∴x取2或3 (6分)
即当甲种机器买2台，此时乙种机器买4台，所需资金为：7×2+5×4=34（万元）；
当甲种机器买3台，此时乙种机器买3台，所需资金为：7×3+5×3=36（万元）；
显然，应选择购买甲种机器2台，乙种机器4台．
答：为了节约资金，应选择购买甲种机器2台，乙种机器4台 (8分)．
27、（1）在直角梯形ABCD中，因AD∥BC，所以只要当DP=CQ时，四边形PQCD为平行四边形(2分)；由题意可得：3t=24-t，t=6（秒）(4分)答：略．
（2）作DE⊥BC， 因为AD=24厘米，BC=26厘米，所以EC=2厘米 (5分) ，
因AD∥BC，当四边形PQCD为等腰梯形时，CQ=DP+2EC (6分)
由题意可得：3t=24-t+4，t=7（秒）(7分)
又因∠B=900，AB=8厘米，所以此时梯形面积S=（17+21）×8/2=152 cm2 (8分) 答：略．