南平市2003--2004学年第二学期期末考试
八年级数学试题
(满分100分,考试时间120分钟)
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 1~12 | 13~17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||
| 得分 | |||||||||||
| 得分 | 评卷人 | 一、填空题(每小题2分,共24分) |
1. ![]() 的立方根是_____________.
的立方根是_____________.
2.某城市地图比例尺为![]() ,该城市滨江大道在图上的距离为21厘米,则其实际长度
,该城市滨江大道在图上的距离为21厘米,则其实际长度
为________________米.
3.已知点![]() 的坐标是
的坐标是![]() ,则它关于
,则它关于![]() 轴的对称点的坐标是______________.
轴的对称点的坐标是______________.
4.当![]() ______________时,二次根式
______________时,二次根式![]() 有意义.
有意义.
5.已知一个三角形的面积为1,一边长为![]() ,这边上的高为
,这边上的高为![]() ,则
,则![]() 关于
关于![]() 的函数关系式
的函数关系式
为__________________.
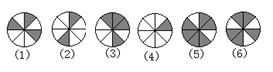 6.把下列自由转动的转盘的序号按转出黑色的机会从小到大的顺序排列起来
6.把下列自由转动的转盘的序号按转出黑色的机会从小到大的顺序排列起来
是________________________________.
7.![]() =___________(
=___________(![]() 为锐角).
为锐角).
8.已知![]() 是反比例函数
是反比例函数![]() 图象上的两点,则
图象上的两点,则![]() .
.
(填“<”、“=”、“>”)
9.一根竹竿的高为1.5 m,影长为1 m,同一时刻,某电视塔影长是20 m,
 则电视塔的高度为______________m.
则电视塔的高度为______________m.
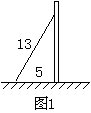
10.已知路灯需安装在12.5米高的灯柱顶端,电工师傅取了一架长
13米的梯子,斜靠在灯柱上(如图1),这时梯子的下端距灯柱底端
5米.你觉得电工师傅能将路灯安上去吗?______ (填“能”或“不能”)
11.两相似三角形对应边上的中线的比为3∶2,较大三角形的面积是12cm2,则较小三角形
的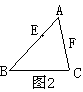 面积为________________.
面积为________________.
12.如图2,在△ABC中,AB>AC,过AB上一点E作直线EF交AC
于F,使得所作的△AEF与原三角形相似,这样的直线最多
可作_______________条.
| 得分 | 评卷人 | 二.选择题:( 每小题3分,共15分) |
下列每小题四个答案中有且只有一个是正确的,请把正确的答案的代号写在题后的括号内.
13.在下列实数中,无理数是----------------------------------------------------------------( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.已知二次根式![]() ,其中与
,其中与![]() 是同类根式的有--(
)
是同类根式的有--(
)
A.3个 B.4个 C.5个 D.6个
15.若点![]() 在第二象限,则
在第二象限,则![]() 的取值范围是--------------------------(
)
的取值范围是--------------------------(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
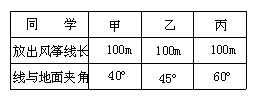 16.三名身高相等的好朋友甲、乙、丙
16.三名身高相等的好朋友甲、乙、丙
周末相约到郊外放风筝,三人放出
的风筝线长及线与地面的夹角如右
表所示(假设风筝线是拉直的),
则三人所放的风筝中------------------------------------------------------------------------( )
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
17.如图3,在平静的湖面上,有一支红莲BA,高出水面的部分AC为1米,一阵
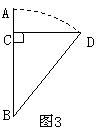 风吹来,红莲被吹到一边,花朵齐及水面(即AB=DB).
风吹来,红莲被吹到一边,花朵齐及水面(即AB=DB).
已知红莲移动的水平距离CD为3米,则湖水深CB为( )
A.12米 B.4米
C.3米
D.![]() 米
米
三、解答题(共61分)
18.化简或计算:(第一小题3分,第二小题4分,共7分)
(1)![]() (2)
(2)![]()
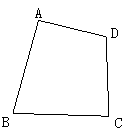
19.(6分)已知四边形![]() ,以
,以![]() 为位似中心,作它的位似四边形
为位似中心,作它的位似四边形![]() ,使四边形
,使四边形![]() 与四边形
与四边形![]() 的相似比为1∶2.(保留作图痕迹,不必写出作法.)
的相似比为1∶2.(保留作图痕迹,不必写出作法.)
 |
20.(6分)暑假里的一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走
了一段路程,爸爸才开始出发.图中两条线段分别表示小军和爸爸离开山脚登山的路程
S(米)与登山所用的时间t(分钟)的关系(从爸爸开始登山 时计时).请你根据图
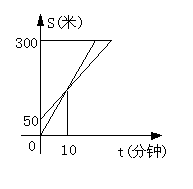 象,至少写出两条信息.(如果多写,每条还可以另加1分哦,但最多只能加2分.)
象,至少写出两条信息.(如果多写,每条还可以另加1分哦,但最多只能加2分.)
| |
21.(6分)为了从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了检
测,两人在相同的条件下各射击10发子弹,命中的环数如下:
甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,7,6,8,6,7,7
假如你是一名教练,请你设计一个较为合理的选拔方案.确定甲、乙两名学生谁
更适合参赛.
22.(8分)一次函数![]() 的图象经过点(1,3)和点(4,6)
的图象经过点(1,3)和点(4,6)
(1)求这个一次函数解析式.
(2)在直角坐标系中画出这个一次函数的图象.并根据图象回答:当![]() 取何值
取何值
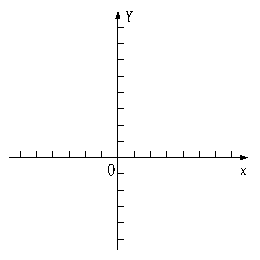 时,①
时,① ![]() ;② 图象在第二象限.
;② 图象在第二象限.
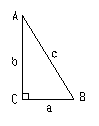 23.(8分)如图,在直角△
23.(8分)如图,在直角△![]() 中,
中,![]() ,
,![]() 分别是
分别是![]()
的对边,![]() 为斜边,如果已知两个元素
为斜边,如果已知两个元素![]() ,就可以求出其余三
,就可以求出其余三
个未知元素![]() .
.
(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程:
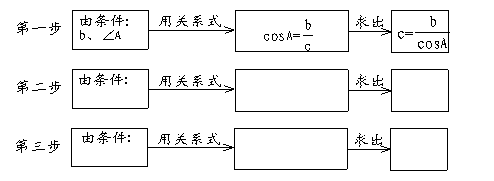 |
(2)若![]() ,然后按照(1)中的思路,求
,然后按照(1)中的思路,求![]() 的值.
的值.
(边长精确到0.01,角度精确到![]() )
)
24.(10分)某校准备在甲、乙两家公司为毕业班学生制作一批纪念册,甲公司提出:每册
收材料费5元,另收设计费1500元;乙公司提出:每册收材料费8元,不收设计费.
(1)请写出甲公司收费![]() (元)与制作纪念册的册数
(元)与制作纪念册的册数![]() 之间的函数关系式.
之间的函数关系式.
(2)请写出乙公司收费![]() (元)与制作纪念册的册数
(元)与制作纪念册的册数![]() 之间的函数关系式.
之间的函数关系式.
(3)如果学校派你去甲、乙两家公司定做纪念册,你会选择哪家公司?
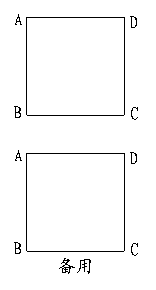
25.(10分)操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),将
一 块三角板的直角顶点与P点重合,并且使一条直角边始终经过点B,另一直角边与正
方形的某一边所在直线交于点E.
探究:(1)观察操作结果,哪一个三角形与△BPC相似?请说明理由;
(2)当点P位于CD的中点时,求(1)中你找到的三角形与△BPC的
周长比是多少?
 |