几何期末综合测试题

几何期末综合测试题

　　

　　【期末综合测试】

　　一、填空

　　1.一梯形的中位线长17，两条对角线互相垂直，并且一条对角线与下底的夹角为30°，则另一条对角线的长为　　　　　  .

　　

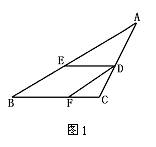
　　2.如图1，菱形BEDF内接于△ABC，若AB＝18，AC＝BC＝12，菱形的边长是　　　　　  .

　　

　　3.△ABC中，AD平分∠BAC交BC于D，DE∥AC交AB于E，EF∥BC交AC于F.若AB＝15cm，AF＝4cm，则BE＝　　　　　　 ，DE＝　　　　　　 .

　　

　　4.顺次连接对角线相等的四边形四边中点所组成的四边形是　　　　　 

　　

　　5.Rt△ABC中，∠C＝90°，CD⊥AB于D，DE⊥AC于E，DF⊥BC于F，BC＝6cm，AC＝8cm，则BF∶AE＝　　　　　  .

　　

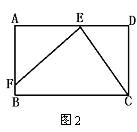
　　6.如图2，矩形ABCD中，E为AD上一点，EF⊥CE交AB于F，若DE＝2，矩形的周长为16，且CE＝EF，则AE＝　　　　　  .

　　

　　7.菱形ABCD中，∠BAC＝60°，则＝　　　　　　　　　 .

　　

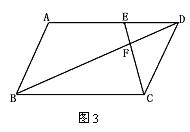
　　8.如图3，□ABCD中，E在AD上，且4AE＝5DE，CE交BD于F，则BF∶DF＝　　　　　  .

　　

　　9.如果△ABC与△DEF的边长分别为6、5、8、与10、、，那么这两个三角形　　　　　  ，根据是　　　　　　　　　　　　　　　　　　　　 .

　　

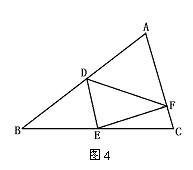
　　10.如上图4，△ABC中，DE∥AC，AB∶DB＝2∶1，F为AC边上任意一点，S_△DEF＝2，则S_△ABC＝　　　　　  .

　　

　　二、选择题

　　1.如图5，已知AB＝AC，∠A＝36°，AB的垂平分线交AC于D，则下列结论①∠C＝72°；②BD是∠ABC的平分线；③△ABD为等腰三角形；④△ACD∽△ABC，其中正确的个数是(　　)

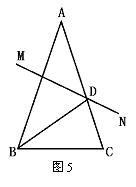
　　A.4个　　　　　　　B.3个　　　　　　 C.2个　　　　　　 D.1个

　　

　　2.下面性质：①对角线互相平分；②对边相等；③对角线互相垂直且相等④对角相等.矩形和菱形同时具有性质是(　　)

　　A.①②④　　　 B.①②　　　　　　 C.②③　　　　　　 D.①④

　　

　　3.在线段、角、等边三角形、平行四边形、矩形、菱形、等腰梯形这些图形中既是轴对称图形，又是中心对称图形的个数是(　　)

　　A.6个　　　　　　 B.5个　　　　　　 C.4个　　　　　　 D.3个

　　

　　4.下列命题中，真命题的是(　　)

　　A.一组对边平行，另一组对边相等的四边形是等腰梯形

　　B.一组对边相等，一组对角相等的四边形是平行四边形

　　C.两条对角线分别平分一组对角的四边形是菱形

　　D.两条对角线互相平分且相等的四边形是正方形

　　

　　5.若∶∶＝2∶3∶4，则a∶b∶c等于(　　)

　　A.4∶3∶2　　　　　B.6∶4∶3　　　　　C.5∶4∶2　　　　　D.3∶4∶6

　　

　　6.正方形ABCD中，E为AD的中点，BE交AC于G，S_△AGE∶S_△BCG∶S_{四边形EGCD}∶S_{正方形ABCD}等于(　　)

　　A.1∶2∶3∶4　　　 B.1∶4∶5∶12　　　C.1∶4∶5∶6　　　 D.1∶4∶5∶9

　　

　　7.如图6，M为□ABCD的边AB的中点，CM交BD于E，则图中阴影部分的面积与□ABCD的面积比是(　　)

　　

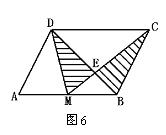
　　A. 　　　　　　　　　B. 　　　　　　　　　C. 　　　　　　　　　D.

　　

　　8.△ABC被平行于BC边的两条线段分成3等分，若BC长为12cm，那么这两条线段中较长的线段为(　　)

　　A.4cm　　　　　　　　　 B.8cm　　　　　　　　　C.4cm　　　　　D.4cm

　　

　　9.如图7，若∠1＝∠2＝∠3，则图中相似三角形共有(　　)

　　

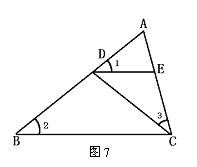
　　A.1　　　　　　　　B.2　　　　　　　　C.3　　　　　　　　　　D.4

　　

　　10.如图8，AB∥CD，AB＝6，CD＝10，若S_梯形ABDC＝128，则S_EAB等于(　　)

　　

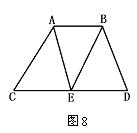
　　A.54　　　　　 B.64　　　　　C.72　　　　　　　 D.78

　　

　　三、解答题

　　1.如图9，△ABC中，BM平分∠ABC，AM⊥BM，垂足为M，点N为AC的中点，设AB＝10，BC＝6，求MN的长度.

　　

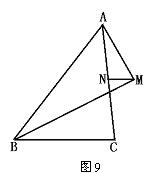
　　2.如图10，梯形ABCD中，AD∥BC，AB＝CD，M、N、P分别为AD、BC、BD的中点，若∠ABD＝20°，∠BDC＝70°，求∠NMP的度数.

　　

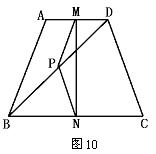
　　3.如图11，CE是Rt△ABC斜边上的高，在EC的延长线上取一点P，连AP，作BG⊥AP于G，交CE于D，求证：CE是ED和EP的比例中项.

　　

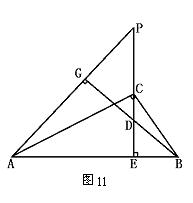
　　四、阅读下面材料，按要求完成后面作业.

　　三角形内角平分线性质定理：三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例.

　　已知：△ABC中，AD是角平分线(如图12)

　　

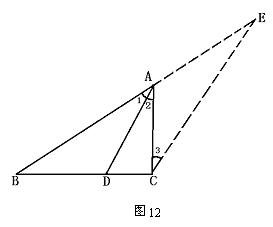
　　求证：＝

　　分析　要证＝，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似，现在B、D、C在一条直线，△ABD与△ADC不相似，需要考虑用别的方法换比.

　　在比例式＝中，AC恰好是BD、DC、AB的第四比例项，所以考虑过C作CE∥AD交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明＝，就可转化证＝

　　1.完成证明过程：

　　证明：

　　2.上述证明过程中，用到了哪些定理(写对两个即可)

　　答：用了①

　　　　　　②

　　3.在上述分析和你的证明过程中，主要用到了下列三种数学思想的哪一种，①数形结合思想　②转化思想　③分类讨论思想

　　答：

　　4.用三角形内角平分线定理解答问题：

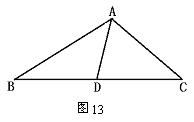
　　如图13，△ABC中，AD是角平分线，AB＝5cm，AC＝4cm，BD＝7cm，求BD之长.

　　

　　参考答案

　　【期末综合测试】

　　一、1.17　2.7.2　3.9cm　6cm  4.菱形  5.27∶64　6.3　7. 　8.9∶4　

　　9.相似  三边对应成比例，两三角形相似　10.8

　　二、1.A　2.A　3.D  4.C　5.B　6.B  7.A　8.D　9.C  10.C

　　三、1.MN＝2(延长BC交AM的延长线于D，先证AB＝BD，再求出CD之长，于是有MN＝CD＝2)

　　2.25°(提示：由∠MPN＝130°

　　再证△PMN为等腰三角形，∴∠NMP＝×(180°－∠MPN)＝25°

　　3.提示：CE²＝ED·EP