仙游金石中学2005―2006学年度上学期第二次月考试卷
八年级数学科
成绩＿＿＿＿＿＿
一、 选择题：（每题4分，共32分）
1．下列函数中，y是x的反比例函数的是（ ）
A. 
B.
C.
D. 
2．若y与x成正比例函数，z与y成反比例函数，则z是x的（ ）
A. 正比例函数 B. 反比例函数 C. 二次函数 D. z随x增大而增大
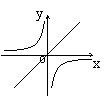
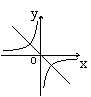
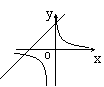
3．正比例函数
和反比例函数
在同一坐标系内的图象可能为( )
 |  | ||||||
 |  | ||||||
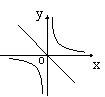A B C D
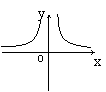
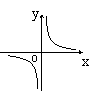
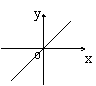
4．如果矩形的面积为6cm2，那么它的长
cm与宽
cm之间的函数关系用图象表示大致（ ）
 |  | ||||||
 | |||||||
 | |||||||
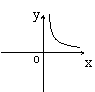A B C D
5．反比例函数（k>0）的图象上有A
、B
两点，若
>0,
则
的大小关系是（ ）
A 
B
C 
D 不能确定
6．在下列线段a,b,c的长为三边的三角形中，不能构成直角三角形的是（ ）
A 
B
|
|
C 
D
|
|
中，AB=13,AC=15,高AD=12,则BC的长是（ ）
A 14 B 4 C 14或4 D 以上都不对 (第8题图)
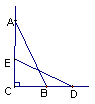
8．如图，四边形ABCD中，AB=3,
BC=4, CD=12, DA=13, 且
，则四边形ABCD的面积为（ ）
A 84 B 36 C 25.5 D 无法确定
二．填空题（每空3分，共39分）
9．三角形的面积为12，底边a与这边上的高h之间的函数关
系式为______________;
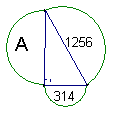
10．如图中字母A所代表的半圆的面积为________________ (第10题图)
11．已知反比例函数
的图象的一支在第一象限，则另一支在第______象限，w的取值范围是__________;
12．双曲线的图象在第一，三象限，则一次函数
过第________象限，在双曲线的每一支上，y随x的增大而__________;
13．反比函数
上有一点P，PQ垂直x轴于Q，则
POQ的面积是_______;
14．已知一个直角三角形的两条直角边分别为6cm,8cm,
那么这个直角三角形斜边上的高为_________;
15．三角形的两边长分别为3和5，要使这个
三角形是直角三角形，则第三边长是________; （16题图）
16．如图所示，一个梯子AB长5米，顶端A靠在墙AC上，这时梯子下端B与墙角C间的距离为3米，梯子滑动后停在DE的位置上，测得DB的长为1米，则梯子顶端A下落了________ 米。
17．有一个边长是1米的正方形洞口，想用一个圆盖去盖住这个洞口，圆的半径至少_________ 米。（结果精确到0.01,
已知
）
18．写出命题“如果两个实数相等，那么它们的绝对值相等”的逆命题：
_________________________________________________
19.现有两根长分别是3cm和4cm木棒，若要钉成一个直角三角形木架,第三根木棒最短长是_______cm
三．解答下列各题
19.(10分)已知变量y与(x+1)成反比例，且当x=3时，y=4，
(1) 求y与x之间的函数关系式;
(2) 求当x=
时y的值
20、（10分）已知直线
与反比例函数
的图象交于A.B两点,且点A的纵坐标为-1,点B的横坐标为2,求一次函数的解析式.
21.(10分) 如图(8)，为修通铁路需凿通隧道AC，测得∠A=55°，∠B=35°，AB=10km，BC=8km，若每天开凿隧道0.3km，试计算需要几天才能把隧道AC凿通？(10分)
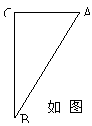
22.(12分)如图，在四边形
中，∠
，，
,CD=13，求四边形的面积.
 |
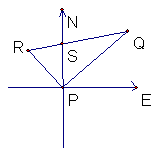23. (10分)“远洋”号,“海天”号轮船同时离开港口,
“远航”号以每小时15海里的速度向东北方向航行，“海天”号以一定的速度向西北方向航行，2小时后，两船相距50海里，求“海天”号的速度？
24.(13分)为了预防“非典”，学校对教室进行消毒，已知药物燃烧时，室内每立方米的含药量 y(毫克)与时间x(分钟)成正比例；药物燃烧后，y与x成反比例
(1) 分别求出药物燃烧时和药物燃烧后y与x的函数关系式
(2) 
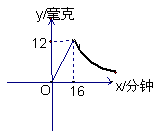药物燃烧后，当空气中每立方米的含药量低于
时,学生方可进入教室,求经过多少分钟学生可进入教室?
25.(14分)市煤气公司要在地下修建一个容积为
的圆柱形煤气储存室.
(1) 储存室的底面积S(单位:
)与其深度d(单位:m)有怎样的函数关系?
(2) 公司决定储存室的底面积S定为250,施工队施工时应向下掘进多深?
(3) 当施工对按(2)中的计划掘到到地下20米时,碰上岩石.为节约资金,公司临时改变计划,把深度改为20m,相应的,储存室的底面积应改为多少?