第四章命题与证明过关性练习（复习2） 第38课时
教学目标：利用课内时间让学生当堂完成这八个题目，教师巡视，了解学生对本章知识点的掌握情况，特别是让学生熟练习掌握完整的证明过程。
时间安排：前25分钟让学生独立完成，后20分钟重点讲解学生出错较多的题目。
1、把下列命题改写成“如果······，那么······”的形式。
⑴对顶角相等；
⑵过一点有且仅有一条直线垂直于已知直线;
⑶等角的角余相等；
⑷在同一平面内，垂直于同一条直线的两条直线平行；
⑸正方形是轴对称图形；
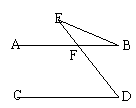2、已知：E是AB、CD外一点，∠D=∠B+∠E，求证：AB∥CD。
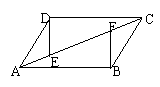
3、如图：已知AD∥BC，AD=BC，AE=CF.求证：DE∥BF
 |
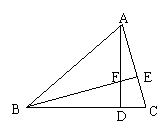4、如图：已知AD为ΔABC的高，E为AC上一点，BE交AD于F，
且有BF=AC，FD=CD，求证：BE⊥AC
5、如图，点B、D、E、C在同一条直线上，且∠1=∠2，BD=EC，
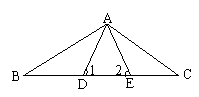求证：ΔABE≌ΔACD
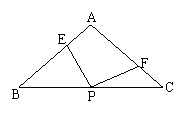
6、如图在ΔABC中AB=AC,∠BAC=900,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F。 ⑴求证：AE=CF
⑵是否还有其它结论。
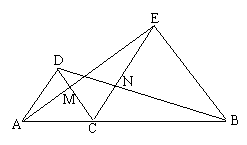7、如图：已知点C在AB上，ΔACD与ΔCBE是等边三角形，连结AD、BE分别交CD、CE于点M、N。求证：（1）AE=BD；
（2）CM=CN。
8、如图：已知等腰直角三角形ABC中,∠ACB=
,直线
经过点C,AD⊥,BE⊥,垂足分别为D、E。
(1)证明ΔACD≌ΔCBE；
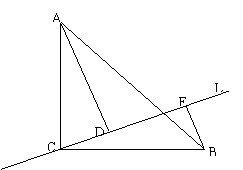
(2)如图，当直线经过ΔABC内部时,其他条件不变,这个结论还是真命题吗?如果是真命题,请给出证明；如果是假命题，请说明理由。