第一、二章综合测试题
一、选择题（每小题4分，共32分）
1、能使等式
成立的a的取值范围（ ）
A、a≥0 B、a＞2 C、a≠2 D、a≤0
2、在方程ax2＋bx＋c＝0（a≠0）中，若a、b、c满足a＋b＋c＝0，且a－b＋c＝0，则方程的根是（ ）
A、1，0 B、-1，0 C、1,-1 D、无法确定
3、对于任意实数，代数式x2－6x＋10的值是一个（ ）
A、非负数 B、正数 C、负数 D、整数
4、化简
，结果正确的是（ ）
A、2x B、0或2x C、－2x或2x D、－2x
5、若代数式x2＋ax＋
是一个完全平方式，则a的值是（ ）
A、
B、
C、－1 D、±1
6、如果x＝3是关于x的方程x2－ax＋9＝0的一个根，则方程的另一个根是（ ）
A、x＝－3 B、x＝0 C、x＝3 D、原方程只有一个根
7、某工厂计划经过两年的时间将某种产品的产量从每年144万台提高到169万台，则每年平均约增长（ ）
A、5％ B、8％ C、10％ D、15％
8、若
，0＜x＜1，则
的值是（ ）
A、
B、－2
C、±2 D、±
二、填空题（每小题4分，共20分）
1、已知a＝8，b＝4，则
＝____________。
2、大于
且小于
的整数有____________ 。
3、已知关于x的方程（m2－4）x2＋（m－2）x－2＝0，当m_____________时，该方程是一元二次方程；当m_____________时，该方程是一元一次方程。
4、若
，则a的值是_______________。
5、在等腰三角形ABC中，BC=8，AB、AC的长是关于x的方程x2－10x＋m＝0的两根，则m的值是_________________。
三、解答题
1、（8分）已知
，
，求a2＋ab＋b2的值。
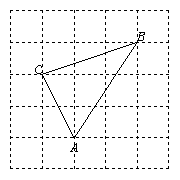
2、（10分）如右图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求点C到AB边的距离。
3、（10分）用配方法说明x2+2mx+2m2+1的值总是大于0。
4、（10分）已知△ABC的两边长为2和3，第三边长为方程x2－7x＋10＝0的根，求△ABC的周长。
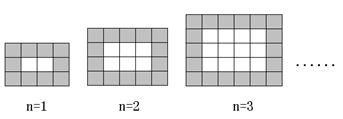
5、（10分）如右图，用同样规格黑白两色的正方形瓷砖铺设地面，请观察右边图形并解答有关问题： （1）在第n个图形中,需用白瓷砖、黑瓷砖各多少块（均用含n的代数式表示）；
（2）按上述的铺设方案，设铺一块这样的矩形地面共用506块瓷砖，且黑瓷砖每块4元，白瓷砖每块3元，问一共需花多少元钱购买瓷砖？
（3）是否存在黑、白瓷砖块数相等的情形？请通过计算说明为什么？