2005学年江干区第一学期8年级期末考试卷
数 学
各位同学:
1、本试卷分试题卷和答题卷两部分，考试时间100分钟,满分120分
2、答题前，请在答题卷的密封区内填写学校、班级和姓名
3、可以使用计算器
4、所有答案都必须做在答题卷规定的位置上，注意试题序号的答题序号相对应
试题卷
一、选择题（每题3分，共30分）
1. 下列日常生活现象中不属于平移的是
（A）飞机在跑道上加速滑行 （B）大楼电梯上上下下地迎送客人
（C）时钟上的秒针在不停的运动 （D）滑雪运动员在平坦的雪地上滑行
2．抛掷一枚普通骰子，出现点数是3的机会是
（A）
（B）
（C）
（D）
3. 平行四边形不一定具有的特征是 （ ）
（A）对角相等 （B）对边相等 （C）对角线相等 （D）对边平行
 |
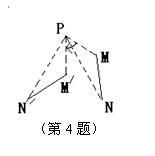4．如图，把线段MN绕点P顺时针旋转60º，
得到线段
，那么，在下面的四个结
论中，错误的是
（A）
＝
（B）△
是等边三角形
（C）∠
=60º （D）
5．以下四边形中，既是轴对称图形又是中心对称图形的是( )
（A）平行四边形 （B）菱形 （C）梯形 （D）等腰梯形
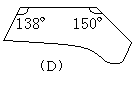
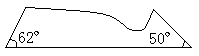6．下列四个图形缺口都能与右边的图形缺口吻合，
哪个图形有可能与右边残缺的图形拼成一个梯形
 |  |
 |  |
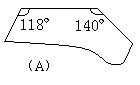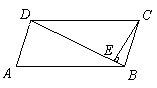7. 如图，在平行四边形ABCD中，BD=CD，
ÐBCE =15°，CE^BD于E，则ÐA等于
（A）75° （B）70°
（C）65° （D）60°
8.下列多项式中，不能用公式
进行分解因式是
（A）
（B）
（C）
（D）
9．满足不等式
＜4的整数有
（A）3个 （B）5个 （C）7个 （D）9个
10．某工地需要爆破，操作人员点燃导火线后，要在爆炸前跑到400米以外的安全区域，已知导火线的燃烧速度是1.2厘米/秒，人跑步的速度是4米/秒，则导火线的长度至少应有
（A）68厘米 （B）96厘米 （C）100厘米 （D）120厘米
二、填空题（每题4分，共24分）
11．小青把自己的左手和右手手心朝下将手印印在同一张白纸上，左手手印通过平移与右手手印_____▲_____完全重合。（填“能”或“不能”）
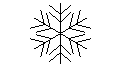
12．如图所示的雪花图形中是旋转对称图形，至少需要绕中心
旋转 ▲ 度，该图形才能与自身重合.
13．如果多项式x2＋mx＋16=
，那么m的值为 _▲_ .
 |
14. 如图，在□ABCD中，对角线AC、BD
相交于O，AC+BD =18，BC=6，则△AOD
的周长为 _▲_
|
|
和石头
相距100cm，且关于竹竿l对称，一只电动青蛙在距竹竿35cm，距石头为65cm的
处，按如下顺序循环跳跃：
 |  | ||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
青蛙跳跃25次后停下，此时它与石头相距 cm.
16．某运动员在一定条件下射击命中的机会是50％，如果她连续射击两次，那么恰有一次射中的机会是 _▲_ .
三、解答题（共66分）
17．计算(每题4分，共12分)
（1）
（2）
（3）
18．因式分解(每题4分，共8分)
（1）
（2）
19．解不等式（组），并将解集在数轴上表示出来(每题6分，共12分)
（1）
（2） 
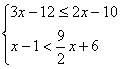
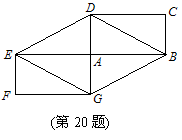
20．(7分)如图，矩形ABCD和矩形AEFG关于点A中心对称，
（1） 四边形BDEG是菱形吗？请说明理由.
（2） 若矩形ABCD面积为2，求四边形BDEG的面积.
 |
21．(9分)
现有一项资助贫困生的公益活动由你来主持，每位参与者需交赞助费5元，活动规则如下：交赞助费5元就可以获得一次转转盘的机会，（转盘分为4个扇形区域，分别是一等奖、二等奖、三等奖、不获奖），转盘指针停在哪个获奖区域就可以获得该区域相应等级奖金。商场工作人员在制作转盘时，将获奖扇形区域圆心角分配如下表：
| 奖次 | 一等奖 | 二等奖 | 三等奖 |
| 圆心角 | 1° | 10° | 20° |
其余均不得奖；此次活动所集到的赞助费除
支付获奖人员的奖金外，其余全部用于资助
贫困生的学习和生活。
（1）分别求出此次活动中获得一等奖、二等奖、三等奖的频率；
（2）若此次活动有3600人参加，活动结束后至少有多少赞助费用于资助贫困生？
（3）如果不用转盘，请设计一个模拟实验方案。（要求写清楚替代工具和实验规则）
22．(5分) 如图，用“●”、“■”表示两个不同的物体，用天平称它们的质量，三次称量情况如图所示,若这两物体的质量是整数,那么“●”、“■”的质量分别是多少克？
 |
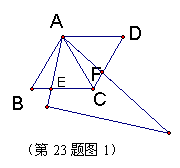
23．(8分)用两个完全相同的正三角形
ABC和ACD拼成菱形，把一个含60º角的三角尺与这个菱形叠合，使三角尺的60º角的顶点与点A重合，两边分别与AB、 AC重合，再将三角尺绕点A按逆时针方向旋转。
（1） 如图（1），当三角尺的两边分别与菱形的两边BC、 CD相交于点E 、F时，通过观察或测量BE、 CF的长度，你能得出什么结论？试说明理由。
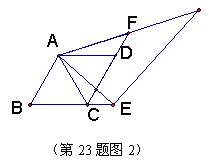
（2） 如图（2），当三角尺的两边分别与菱形的两边BC、 CD的延长线相交于点E、 F时，你在（1）中得到的结论还成立吗？简要说明理由。
 |  |
24．（5分）已知：有理数x、y、z满足
，
，试说明x = y.