市2004学年第二学期八年级期末测试
数 学 试 卷
亲爱的同学,这份试卷将再次记录你的自信、沉着、智慧和收获. 我们一直投给你信任的目光,请你认真审题,看清要求,仔细答题. 凡解答题都应有必要的步骤.
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||
| (1-10) | (11-20) | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | ||
| 得 分 | |||||||||||
| 评卷人 | |||||||||||
一、细心填一填,把正确答案填在横线上(本题有10小题,每小题2分,共20分)
 1、4的平方根是
.
1、4的平方根是
.
2、函数![]() 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
3、请你写出一个比2大的无理数: .
4、在直角DABC中,∠C=90°,sinA=![]() ,则cosB=
.
,则cosB=
.
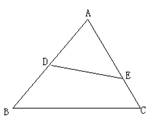
5、如图,下列条件: ①∠AED=∠B;②DE:BC=AD:AC;③AD:AC=AE:AB;
④∠ADE=∠C,其中能判断DADE∽DACB的是 .(填上所有正确的序号)
6、在一副52张(没有大小王)的扑克中任意抽取1张,将下列事件发生的机会按从小到大排序:抽出的这张纸牌是(1)红色;(2)大王;(3)不是A.答:应为 .
7、直线y=-x+m与直线y=4x-1交于x轴上一点,则m= .
8、沿倾斜角为300的山坡植树,要求相邻两棵树间的水平距离为2米,则相邻两棵树间的斜坡距离为 米.(精确到0.1米,可能用到的数据:![]() )
)
9、如图,已知直线y=-x+2分别交x轴、y轴于点A、B,OC⊥AB,垂足为C,若∠AOC=α,
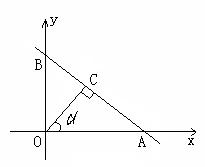
 则sinα=
.
则sinα=
.
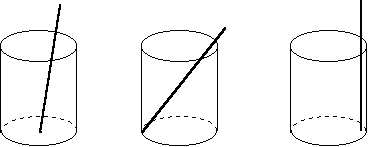
10、如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是 .
二、精心选一选,相信自己有能力选得又快又准.(注意只有一个是对的,将正确答案相对应的序号填在括号里)!(本大题有10小题,每小题3分,共30分)
11、![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、下列各式正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
13、下列四组线段中,不构成比例线段的一组是( )
A、1cm,2cm,3cm,6cm B、2cm,3cm,4cm,6cm
C、1cm,![]() D、1cm,2cm,3cm,4cm
D、1cm,2cm,3cm,4cm
14、为鼓励居民节约用水,春海市将出台新的居民用水收费标准:(1)若每月每户居民用水不超过4立方米,则按每立方米2元计算;(2)若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水x立方米,水费y元,则y与x的函数关系用图象表示正确的是( )
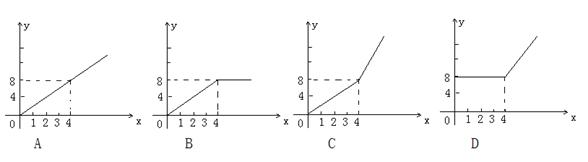 15、数学老师对小芳参加中考前的5次数学成绩进行统计分析,判断小芳的数学成绩是否稳定,于是老师需要知道小芳这5次数学成绩的( )
15、数学老师对小芳参加中考前的5次数学成绩进行统计分析,判断小芳的数学成绩是否稳定,于是老师需要知道小芳这5次数学成绩的( )
A、平均数或中位数 B、方差或极差 C、众数或频率 D、频数或众数
 16、在DABC中,∠C=90°,延长CA至D,使AD=AB,∠BAC=30°,则cot75°的值是 ( )
16、在DABC中,∠C=90°,延长CA至D,使AD=AB,∠BAC=30°,则cot75°的值是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
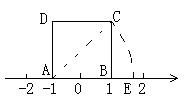
17、如图,ABCD为正方形,以A为圆心,AC长为半径画弧交数轴于点E,则E点所表示的数为( )
A、![]() B、
B、![]()
C、1.8 D、![]()
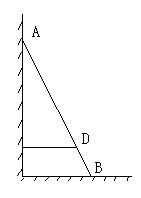
18、如图,AB是斜靠在墙壁上的长梯,梯脚B距墙壁1.6米,梯子上的一点D距墙壁1.4米,量得BD长为0.55米,则梯子长为 ( )
 A、3.85米 B、4.00米 C、4.40米 D、4.50米
A、3.85米 B、4.00米 C、4.40米 D、4.50米
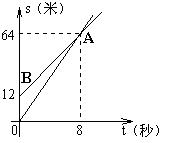
19、如图,OA,BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )
A、1米 B、1.5米 C、2米 D、2.5米
20、若M(![]() 、N(
、N(![]() 、P(
、P(![]() 三点都在函数
三点都在函数![]() 的图象上,则
的图象上,则![]() 、
、![]() 、
、![]() 的大小关系为(
)
的大小关系为(
)
A、y2>y3>y1 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y1
三、沉着思考,耐心解答好下列各题(有8个题,共50分)
21、计算: ![]() (本题4分)
(本题4分)
22、(本题7分)春晖集团为了解职工的阅读情况,在全单位职工中进行了抽样问卷调查,调查职工每周去阅览室的次数.下图是根据调查结果绘制的统计图.解答下列问题:
(1)这种统计图称为 统计图;
(2)共有 名职工接受调查并上交了问卷;
(3)从图中可知接受调查的职工中,每周去阅览室5次以上(含5次)的人数为 ;
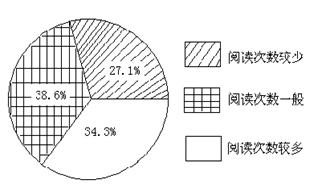
(4)如果1——2次为较少,3——4次为一般,5次及5次以上为较多,请按以上三种情况,将此统计图绘制成扇形统计图;
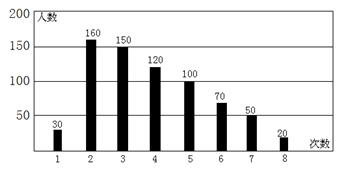 (5)从图中你能获得有关该单位职工阅读情况的哪些信息?
(5)从图中你能获得有关该单位职工阅读情况的哪些信息?
23、(本题6分)地基在同一水平线上的两幢大楼相距100米,从甲楼顶部看乙楼顶部的仰角为32°,如果甲楼高35米,那么乙楼的高为多少米?
(参考数据:sin320»![]() ,cos320»
,cos320»![]() ,tan320»
,tan320»![]() ,精确到1米)
,精确到1米)
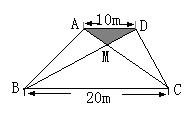
24、(本题6分)卧龙社区居民筹集资金1600元,计划在一块上、下两底分别为10![]() 、20
、20![]() 的梯形空地上种植花木(如图).
的梯形空地上种植花木(如图).
(1)他们在△AMD和BMC地带上种植太阳花,单价为8元/![]() .当△AMD地带种满花后(图中阴影部分)共花了160元.请计算种满△BMC地带所需的费用.
.当△AMD地带种满花后(图中阴影部分)共花了160元.请计算种满△BMC地带所需的费用.
 (2)若其余地带选择玫瑰和茉莉花中的一种进行种植,单价分别为12元/
(2)若其余地带选择玫瑰和茉莉花中的一种进行种植,单价分别为12元/![]() 和10元/
和10元/![]() ,应选择种哪种花木,刚好用完所筹集的资金?
,应选择种哪种花木,刚好用完所筹集的资金?
25、(本题6分)某汽车停车场预计“十·一”国庆节这天将停放汽车1200辆次,该停车场的收费标准是:大车每辆次10元,小车每辆次5元,根据预计,解答下面的问题:
(1)写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式,并指出自变量x的取值范围;
(2) 如果国庆节这天停放的小车辆次占停车总辆次的65%——85%,请你估计国庆节这天该停车场收费金额W的范围.
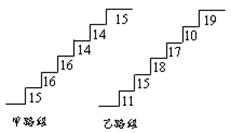
 26、(本题6分)在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
26、(本题6分)在某旅游景区上山的一条小路上,有一些断断续续的台阶.如图是其中的甲、乙段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
 (3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
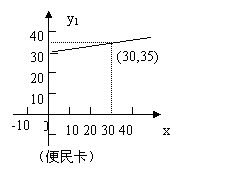
27、(本题7分)为发展电信事业,方便用户,A地电信公司对移动电话采用不同的收费方式,其中,所使用的“便民卡”和“如意卡”每月(30天)的通讯时间x(分钟)与通话费(y元)的关系如图所示:
(1) 分别求出通话费y1、y2与通话时间x之间的函数关系式.
(2) 在A地的林小姐准备购买一部移动电话,并决定选用“便民卡”和“如意卡”中的一种付费方式进行消费.请你帮助林小姐分析应选哪种卡合算.
 |
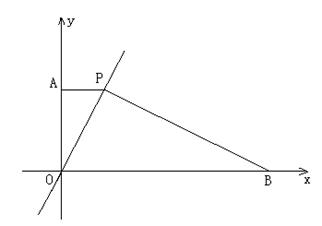
28、(本题8分)如图,P为正比例函数图象上的一点,PA⊥y轴,垂足为A,PB⊥OP与x轴交于点B.
(1)你能得出OP2=PA·OB的结论吗?请说说你的理由;
(2)若P点的横坐标为1,B点的横坐标为5,试求tan∠POB的值;
(3)在(2)的条件下,试问:在线段OP上是否存在这样的点M,使SDMAP:S四边形AOBP=![]() ?若存在,请求出点M的坐标;若不存在,请说明理由.
?若存在,请求出点M的坐标;若不存在,请说明理由.
市2004学年第二学期八年级数学期末测试卷
参考答案及评分意见
一、填空题:(本题有10小题,每小题2分,共20分)
1、![]() ; 2、x≥1; 3、如
; 2、x≥1; 3、如![]() 等; 4、
等; 4、![]() ; 5、①③④; 6、(2)(1)(3);
; 5、①③④; 6、(2)(1)(3);
7、![]() ; 8、2.3 9、
; 8、2.3 9、![]() ; 10、11cm≤h≤12cm;
; 10、11cm≤h≤12cm;
二、选择题:(本题有10小题,每小题3分,共30分)
11、A 12、C 13、D 14、C 15、B 16、A 17、D 18、C 19、B 20、B
三、解答题:(有8个题,共50分)
21、(本题4分)(1)解:原式=![]() (2分+2分=4分)
(2分+2分=4分)
22、(本题7分)(1)条形;(1分) (2)700;(1分) (3)240;(1分)
(4)如图;(3分) (5)略.(1分)
23、(本题6分)由tan320»![]() =
=![]() (3分)得
(3分)得![]()
![]() »98,那么乙楼的高为98米.(6分)
»98,那么乙楼的高为98米.(6分)
24、(本题6分)(1)解:由梯形 ABCD中AD//BC得:△ADM∽△CMB(1分),则
ABCD中AD//BC得:△ADM∽△CMB(1分),则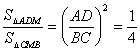 (2分),所以种满△BMC地带所需费用为:
(2分),所以种满△BMC地带所需费用为:![]() 元(3分,根据面积得8×80=640元也可)(2)由△ADM∽△CMB得
元(3分,根据面积得8×80=640元也可)(2)由△ADM∽△CMB得![]() (4分),而△ADM与△AMB的高相等,故
(4分),而△ADM与△AMB的高相等,故![]() ,而
,而![]() 所以
所以![]() (5分),剩余资金为1600-160-640=800元,故选择的花木单价为
(5分),剩余资金为1600-160-640=800元,故选择的花木单价为![]() ,所以应选择种茉莉花(6分).
,所以应选择种茉莉花(6分).
25、(本题6分)(1)设停放小车x辆,则大车停放(1200-x)辆,故y=10(1200-x)+5x,
即y=-5x+12000,其中0≤x≤1200,x为整数.(3分)
(2)1200×65%=780,1200×85%=1020, 当780≤x≤1020时,6900≤y≤8100,
即6900元≤W≤8100元.(6分)
26、(本题6分)解(1)![]()
![]() (1分)又因为
(1分)又因为![]() ,
,![]() (2分)
(2分)
∴相同点:两段台阶路高度的平均数相同. (3分)
不同点:两段台阶路高度的中位数、方差和极差均不相同. (4分)
(2)甲路段走起来更舒服一些,因为它的台阶高度的方差小.(5分)
(3)每个台阶高度均为15cm(原平均数),使得方差为0. (6分)
27、(本题7分)(1)![]() (4分).(2)当通话时间
(4分).(2)当通话时间
![]()
![]() 选择如意卡(7分).
选择如意卡(7分).
28、(本题8分)(1)能得到OP2=PA·OB. 理由是: ∵PA⊥y轴,PB⊥OP于P, ∴∠BPO=∠PAO=Rt∠,又∵PA∥x轴, ∴∠APO=∠BOP, ∴DAPO∽DPOB, ∴![]() ∴OP2=PA·OB.(2分)
∴OP2=PA·OB.(2分)
(2)∵P、B的横坐标分别为1、5, ∴AP=1,OB=5,
故由OP2=PA·OB得: OP2=1×5=5, ∵OP>0,
∴OP=![]() ,
,
在RtDPOB中, OP=![]() ,OB=5, ∴PB=
,OB=5, ∴PB=![]()
∴tan∠POB=![]() . (5分)
. (5分)
(3)存在满足条件的点M. (6分)
∵SDAOP=1,SDOPB=5, ∴S四边形AOBP=1+5=6,
在RtDAOP中,AP=1,OP=![]() 故AO=2,
故AO=2,
设点M的纵坐标为ym ,则
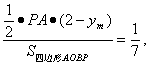 即
即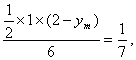 解得:ym=
解得:ym=![]() .(7分),
.(7分),
最后得点M的坐标为(![]() ,
,![]() ).(8分)
).(8分)