初二数学竞赛试卷
（满分150分，考试时间 100分钟）
一、填空题：（每小题8分，共48分）
 |
1．如图，如果 所在位置的坐标为(-1,-2),
所在位置的坐标为(2,-2), 那么， 所在位置的坐
 |
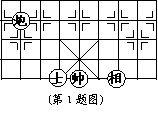标为 .
2．若规定运算 
，则
__________。
3．在计算一个正数乘以
的运算时,某同学误将错写成3.57,
结果与正确的答案相差1.4,则正确的乘积结果是_______.
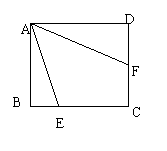
4．正方形ABCD中，点E、F分别在BC、CD上，
且∠EAF=450，已知BE=2，DF=3，则正方形的边长是
5．若
的展开式经同类项合并后至少有2004项，则最小的正整数n的值为
6．若a, b均为正数,且
是一个三角形的三条边的
长,那么这个三角形的面积等于
二、选择题：（每小题8分，共48分）
1．已知 68 9□□□20 312≈690亿（四舍五入），那么其中三位数□□□有（ ）种填写的方法。
（A）1 000 （B）999 （C）500 （D）499
2．在平行四边形ABCD中，AB＝6，AD＝8，∠B是锐角，将△ACD沿对角线AC折叠，点D落在△ABC所在平面内的点E处。如果AE过BC的中点，
则平行四边形ABCD的面积等于 （ ）
A、48 B、
C、
D、
3．如图1,在一个正方体的顶点处填上1～9的数码中的8个,每顶点
只填一个数码,使得正方体每面上的四个顶点所填的数码之和均为18,那么未被
填上的数码是 （ ）
（Ａ）3 (B)5 (C)7 (D)9
4．若关于χ的方程
无解，
只有一个解，
有两个解，则m，n，k的大小关系
（
）（A）
； （B）
； （C）
； （D）
；
5．今有带余除法算式A÷B=C……8，如果A+B+C=2178，那么A=（ ）
（A）2000 （B）2001 （C）2071 （D）2100
6．高斯函数
表示不超过
的最大整数，如
，
，
。求解含高斯符号的方程
的所有根的和是
（ ）
（A）—2 （B）—1。75 （C）—1。25 （D）—0。75
三．解答题（四道大题，共54分）
1．某商店有幸福金笔和英雄金笔共143支，幸福金笔每支6元，英雄金笔每支3.78元。某学校购了该商店的全部英雄金笔和部分幸福金笔，经过核算后，发现应付款的总数与幸福金笔的总数无关，问购买的幸福金笔是该商店幸福金笔总数的百分之几？应付款的总数是多少元？（12分）
2．从等腰Rt△ABC的直角顶点C向中线BD作垂线，交BD于F，交AB于E，连结DE。 求证：∠CDF=∠ADE。（12分）
3．己知一个凸十一边形由若干个边长为1的等边三角形和边长为1的正方形无重叠，无间隙拼成，求该凸十一边形的各内角的大小。（15分）
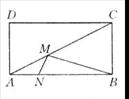
4．矩形ABCD中，AB=20，BC=10，若在AC、AB上各取一点M、N（如图），使BM+MN的值最小，求这个最小值。（15分）
参考答案：
一、填空题：（每小题8分，共48分）
1．（—3 ， 1）
2．
提示：
。
3．乘积为 644
提示:设某正数为x,则
所以，乘积为
644
4．边长是6
提示:将ADF旋转至使AD与AB重合即可
5．n的值为44
提示:将底数进行因式分解
6．这个三角形的面积等于3/2 a b
提示:构造边长为2a,2b矩形
二、选择题：（每小题8分，共48分）
1．选择C
解 可填500，501，502，…，999，共500种填法。选C。
2．选择C
3．选择D
提示:设所填8个数之和为S,每一数出现在3个面上,共有6个面,则得3S=6×18,即S=36.而1+2+…+9=45,故未知数被填上的数码为45-36=9.
4．选择（A）
解：无解，则
有一个解，则
有两个解，则
。 所以
5．选A
解 由已知A=BC+8，代入得BC+B+C+8=2178，故BC+B+C+1=2171，
即（B+1）（C+1）=13×167。因为13与167均为质数，所以只有
或
。 故
，或
。
都可得A=BC+8=166×12+8=2000。
6．解：设
（t为整数。）
则
,
因为
即
, 
t=-2, -3
对应的为
,
。从而原方程所有根的和
三．解答题（三道大题，共54分）
1．解：设购买幸福金笔占幸福金笔总数的百分比为x ,幸福金笔总数为m支，付款总数为T元，则由题意得
∵ T与m 无关，
∴ 
，
，
这时 T=540.54（元）。
2．思路1：作∠BCA的平分线交BD于G，证明△CDG≌△ADE。
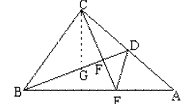
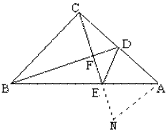
证法1：作∠BCA的平分线交BD于G，
∵
BC=AC，∠BCG=∠A=
， ∠CBG=
-∠CDF=∠ACE，
∴ △BCG≌△CAE，
∴ CE=AE，
△CDG和△ADE中，
∵
CD=AD，∠DCE=∠A=，CE=AE，
∴ △CDG≌△ADE，
∴ ∠CDF=∠ADE，
思路2：过A作AN⊥AC，交CE延长线于N，
证明 △ADE≌△ANE。
证法2：过A作AN⊥AC，交CE延长线于N。
∵ ∠ACN=∠CBD，AC=CB，
∴ Rt△ACN≌Rt△CBD，
∴ ∠CDF=∠ANE，CD=AN=AD，
又∵ ∠CAE=∠EAN=，AE=AE，
∴ △ADE≌△ANE，
∴ ∠ADE=∠ANE，
∴ ∠CDF=∠ADE，
3．解
设此凸十一边形的各个内角中有 x个
y个
z个
s个
由题意有
由①得
代②入化简得
因为
均为非负整数，
所以
故
=10.
则这个凸十一边形有一个角是，有十个内角都是。
4．如图，作B关于AC的对称点B′，连结AB′，则N关于AC的对称点N′在AB′上，过B作AB′的垂线，垂足为H′，则BM+MN=BM+MN′≥BH′，即BM+MN的最小值为BH′。
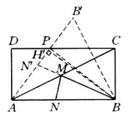
设AB′交CD于点P，连结BP，则△ABP的面积等于
，由AB∥CD及由对称性知∠PAC=∠PCA，
∴AP=PC，设AP=PC=x，则DP=20-x，根据勾股定理，得
，解得x=12.5。
又
，
∴
。
故BM+MN的最小值是16。