§13.4 探究与整理
知识要点
本章主要内容是三角形全等的判定和应用．
1．全等三角形的性质：全等三角形的对应边相等，对应角相等．
2．三角形全等的条件：
（1）一般三角形：①三边对应相等（SSS）；②两边和夹角对应相等（SAS）；③两角和一条边对应相等（ASA或AAS）．
（2）直角三角形：除一般三角形的判定方法外，另外：斜边和一条直角边对应相等（HL）．
3．角平分线性质定理：在角的平分线上的点到这个角的两边的距离相等．
角平分线判定定理：到一个角的两边的距离相等的点在这个角的平分线上．
典型例题
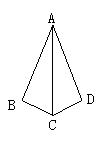
例：如图，已知△ABC中∠BAC=90°，AB=AC，CD垂直于∠ABC的平分线BD于D，BD交AC于E，求证：BE=2CD．
分析：要证BE=2CD，想到要构造等于2CD的线段，结合角平分线，利用翻折的方法把△CBD沿BD翻折，使BC重叠到BA所在的直线上，即构造全等三角形（△BCD≌△BFD），然后证明BE和CF（2CD）所在的三角形全等．
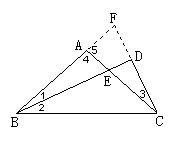证明：延长BA、CD交于点F
∵BD⊥CF（已知）
∴∠BDC=∠BDF=90°（垂直的定义）
∵BD平分∠ABC（已知）
∴∠1=∠2（角平分线的定义）
在△BCD和△BFD中
∴△BCD≌△BFD（ASA）
∴CD=FD（全等三角形的对应边相等） 即CF=2CD
∵∠5=∠4=90°，∠BDF=90°
∴∠3+∠F=90°，∠1+∠F=90°（直角三角形两锐角互余）
∴∠1=∠3（同角的余角相等）
在△ABE和△ACF中
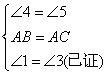
∴△ABE≌△ACF（ASA）
∴BE=CF（全等三角形对应边相等）
∴BE=2CD（等量代换）
同步练习
一、选择题
1．到三角形三边的距离相等的点是三角形（ ）
A．三条边上的高的交点 B．三个内角平分线的交点
C．三边上的中线的交点 D．以上结论都不对
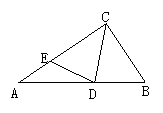
2．如图1，△ABC中，AC⊥CB，CD平分∠ACB，点E在AC上，且CE=CB，则下列结论：①CD平分∠BDE；②BD=DE；③∠B=∠CED；④∠A+∠CED=90°．其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
（1） (2) (3) (4)
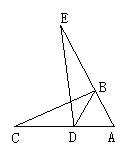
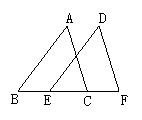
3．如图2，已知点D是△ABC中AC边一点，点E在AB延长线上，且△ABC≌△DBE，∠BDA=∠A．若∠A：∠C=5：3，则∠DBE的度数是（ ）
A．100° B．80° C．60° D．120°
二、填空题
4．△ABC中AB=AC，点D是∠BAC平分线上一点，且BD=2cm，则点D与点C之间的距离是___________．
5．如图3，∠ABC=∠ADC=90°，要证明△ABC≌△ADC，可补充条件___________或____________（填写两组适合的条件即可）．
6．如图4，△DEF由△ABC沿直线BC平移而得到的，则AB=______，CF=_______，∠A=_______．
三、解题题
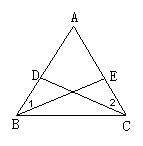
7．如图，D、E是△ABC中AB、AC边上的点，且AD=AE，∠1=∠2，求证BD=CE．
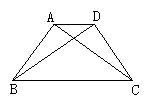
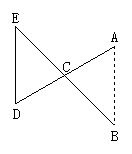
8．如图，已知AB⊥AC于A，BD⊥DC于D，要想得到AC=BD，你认为需要补充什么条件？请说明你的理由．
9．如图，A、B两点分别位于池塘两侧，小亮用下面的方法测量A、B之间的距离：先在地上取一个可以直接到达A点和B点的C点，连接AC、BC，并分别延长至D、E两点，使DC=AC，EC=BC．那么量出DE的长就是A、B间的距离．请说明一下这样做的道理．
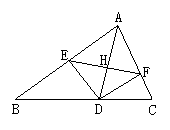
10．如图1，AD是△ABC的角平分线，DE和DF分别是△ABD和△ACD的高，求证：AD垂直平分EF．
答案:
1．B 2．D 3．A 4．2cm 5．AB=AD；∠BAC=∠DAC
6．DE；BE；∠D
7．先证△ABE≌△ACD得到AB=AC，再用等式性质证明BD=CE
8．比如：AB=DC或∠ABC=∠DCB或∠ACB=∠DBC
9．证△ABC≌△DEC
10．证△AEH≌△AFH