2005-2006 学年下学期八年级前三章数学考试
一、运算题：本大题共10小题，共50分，解答应写出必要的计算过程、推演步骤或文字说明．
1.(本小题5分) （1）
满足什么条件时，分式
有意义？
（2）取何值时，分式
无意义？（3）取何值时，分式
的值为零？
2.(本小题5分) 求不等式
的非负整数解．
3.(本小题5分) 把
分解因式．
4.(本小题5分) 用简便方法计算．
．
5.(本小题5分) 用适当的符号表示下列关系：
（1）
是正数；（2）
是非负数；
（3）的一半小于
；（4）
与2差比它的
倍小．
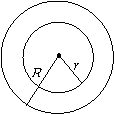6.(本小题5分) 如图，一个圆环，外圆的半径为
，内圆的半径为
．
（1）写出圆环面积的计算公式；
（2）当
cm，
cm时，求圆环的面积（结果保留
）．
7.(本小题5分) 解不等式组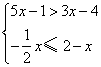
并求它的整数解的和．
8.(本小题5分) 把下列各式分解因式．
（1）
； （2）
．
9.(本小题5分) 若多项式
可分解为
，试求
的值．
10.(本小题5分) 如果不等式
的正整数解是
，那么
的取值范围是什么？并在数轴上表示出来．
二、合情推理题：本大题共2小题，共20分，解答应写出必要的计算过程、推演步骤或文字说明．
11.(本小题10分)
| 造型 | 甲 | 乙 |
|
| 90盆 | 30盆 |
|
| 40盆 | 100盆 |
为美化青岛，创建文明城市，园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配
、
两种园艺造型共50个，摆放在迎宾大道两侧．搭配每个造型所需花卉情况如右表所示：
结合上述信息，解答下列问题：
（1）符合题意的搭配方案有哪几种?
（2）若搭配一个种造型的成本为1000元，搭配一个种造型的成本为1200元，试说明选用（1）中哪种方案成本最低？
解：（1）
12.(本小题10分) 某校初三（2）班课题研究小组对本校初三段全体同学的体育达标（体育成绩60分以上，含60分）情况进行调查．他们对本班50名同学的体育达标情况和其余班级同学的体育达标情况分别进行调查，数据统计如下：
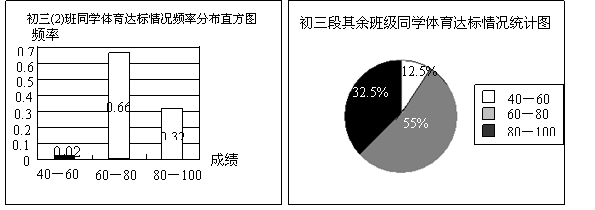
说明：每组成绩的取值范围中，含最低值，不含最高值．
根据以上统计图，请解答下面问题：
（1）初三（2）班同学体育达标率和初三段其余班级同学体育达标率各是多少？
（2）如果全段同学的体育达标率不低于90％，则全段同学人数不超过多少人？
三、证明题：本大题共2小题，共20分，解答应写出必要的计算过程、推演步骤或文字说明．
13.(本小题10分) 在菱形
中，点
在
上，若
．请说明：
平分
．如图所示．
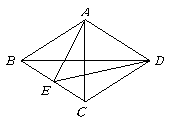
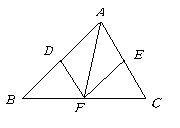
14.(本小题10分) 如图所示，已知
中，
平分
．
（1）你能判断四边形
是菱形吗？并说明理由．
（2）满足什么条件时，四边形是正方形．
 |
四、运算题：本大题共2小题，共20分，解答应写出必要的计算过程、推演步骤或文字说明．
15.(本小题10分) 用适当的符号表示下列关系：
（1）甲比乙矮；
（2）某校八年级人数比七年级人数多．
16.(本小题10分) 将下列不等式化成“
”或“
”的形式．
（1）
； （2）
；
（3）
； （4）
．
五、应用题：本大题共2小题，共10分，解答应写出必要的计算过程、推演步骤或文字说明．
17.(本小题5分) 下表给出甲、乙、丙三种食物的维生素
的含量及成本：
| 甲 | 乙 | 丙 | |
| 维生素 | 400 | 600 | 400 |
| 维生素 | 800 | 200 | 400 |
| 成本（元/千克） | 6 | 5 | 4 |
某食物营养研究所将三种食物混合成110千克的混合物，使之至少需含48 400单位的维生素及52 800单位的维生素．求三种食物所需量与成本的关系式．
18.(本小题5分) 某校八年级（1）班共有56人，期中考试数学及格人数为人，恰好符合学校要求的及格率不低于
的要求．试用关于的不等式表示该班及格人数．
2005-2006 学年下学期八年级前三章数学考试答案
一、运算题：本大题共10小题，共50分，解答应写出必要的计算过程、推演步骤或文字说明．
1.(本小题5分) 解：（1）由分母
，得
．
所以，当取以外的任何实数时，分式有意义．
（2）由分母
，得
．
所以，当时，分式无意义．
（3）由分子
，得
或
．
由分母
，得．
所以，当时，分式的值为零．
2.(本小题5分) 
，取
3.(本小题5分) 解：
4.(本小题5分) 40 000
5.(本小题5分) 解：（1）
．
（2）是非负数，就是不是负数，它可以是正数或零，即
或
，通常可以表示成
．
（3）
．
（4）
．
6.(本小题5分) 解：（1）
．
（2）
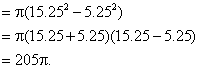
7.(本小题5分) 解：原不等式化为：
解得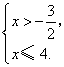
所以原不等式组的解集为
．
此不等式组的整数解为：
、0、1、2、3、4．
所以，这些整数解的和为9．
8.(本小题5分) 解：（1）
（2）
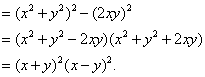
9.(本小题5分) 解：由题意，得
．
而
，
所以
．
比较两边系数，得
．
10.(本小题5分) 
 |
二、合情推理题：本大题共2小题，共20分，解答应写出必要的计算过程、推演步骤或文字说明．
11.(本小题10分) 解：（1）设需要搭配个种造型，则需要搭配
个种造型．
由题意得：
解得：
其正整数解为：
，
，
符合题意的搭配方案有3种，分别为：
第一种方案：种造型30个，种20个；
第二种方案：种造型31个，种19个；
第三种方案：种造型3２个，种18个．
（2）由题意知：三种方案的成本分别为：
第一种方案：
第二种方案：
第三种方案：
第三种方案成本最低
12.(本小题10分) 解：（1）初三（2）班体育成绩达标率为
其余班级体育成绩达标率为
答：初三（2）班同学体育达标率和其余班级同学体育达标率分别是98％和
．
（2）设全段有名同学，由题意得：
解得
答：全段同学人数不超过210人．
三、证明题：本大题共2小题，共20分，解答应写出必要的计算过程、推演步骤或文字说明．
13.(本小题10分) 提示：
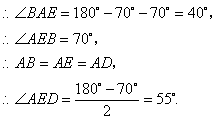
本小题10分) （1）四边形
是菱形．
因为
，故四边形为平行四边形．
又
平分，
又
，
故
所以
．
因为平行四边形的一组邻边相等，所以是菱形．
（2）当满足
时，
四边形为正方形（有一角为直角的菱形是正方形）．
四、运算题：本大题共2小题，共20分，解答应写出必要的计算过程、推演步骤或文字说明．
15.(本小题10分) 解：（1）
（
表示甲的身高，
表示乙的身高）．
（2）
（表示八年级人数，表示七级年人数）．
16.(本小题10分) 解：（1）根据不等式的基本性质1，两边都加上5，得
，即
．
（2）根据不等式的基本性质1，两边都减去，得
，即
．
根据不等式的基本性质3，两边都除以2，得
．
（3）根据不等式的基本性质2，两边都乘以2，得
．
（4）根据不等式的基本性质3，两边都除以
，得
．
五、应用题：本大题共2小题，共10分，解答应写出必要的计算过程、推演步骤或文字说明．
17.(本小题5分) 解：设需甲、乙两种食物分别为
千克，则丙需
千克，设共需成本
元，
应有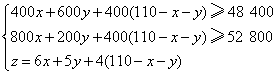
18.(本小题5分) 解：由题意应有
，即
．
又因为应为正整数，故有
．