相似图形精选练习
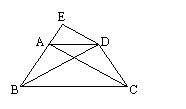1、已知：如图，在等腰梯形ABCD中，AD∥BC，AB＝DC，过点D作AC的平行线DE，交BA的延长线于点E．
求证：（1）△ABC≌△DCB；（2）DE·DC＝AE·BD．
2、如图，在△ABC中，∠CAB=60°，点D是△ABC内的一点，使∠CDA=∠ADB=∠CDB.
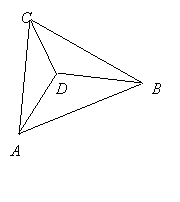求证：线段DA是线段DB、DC的比例中项.
3、如图，在Rt△ABC中，∠ACB=90°，边AC的垂直平分线EF交AC于点E，交AB于点F，BG⊥AB，交EF于点G．
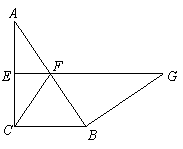求证：CF是EF与FG的比例中项．
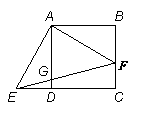4、如图，在正方形ABCD中，F是BC上一点，EA⊥AF，AE交CD的延长线于E，连结EF交AD于G.
（1）求证：⊿ABF ≌⊿ADE；
（2）求证：BF·FC ＝DG·EC；
5、如图3，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，DE=DF，∠EDF=∠A．
（1）找出图中相似的三角形，并证明；
（2）求证：
．
6、如图，△ABC中D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD，E为垂足，连结AE.
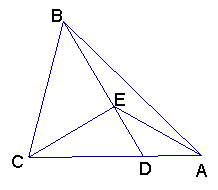求证：(1) ED=DA；(2)∠EBA＝∠EAB；(3) BE2=AD·AC
7、如图△ABC中，∠B=∠C=α（0<α<600）.将一把三角尺中300角顶点P放在BC边上，当P在BC边上移动时，三角尺中300角的一条边始终过点A，另一条边交AC边于点Q，P、Q不与三角形顶点重合.设∠CPQ=β.
（1）用α、β表示∠1和∠2；
（2）①当β在许可范围内变化时，α取何值总有△ABP∽△PCQ？
②当α在许可范围内变化时，β取何值总有△ABP∽△QCP？
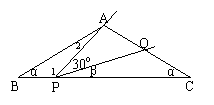（3）试探索有无可能使△ABP、△QPC、△ABC两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由.
参考答案：
1、证明：（1）∵四边形ABCD是等腰梯形，∴AC＝DB，
∵AB＝DC，BC＝CB，∴△ABC≌△BCD，
（2）∵△ABC≌△BCD，∴∠ACB＝∠DBC，∠ABC＝∠DCB，
∵AD∥BC，∴∠DAC＝∠ACB，∠EAD＝∠ABC，
∵ED∥AC，∴∠EDA＝∠DAC，
∴∠EDA＝∠DBC，∠EAD＝∠DCB， ∴△ADE∽△CBD，
∴DE︰BD＝AE︰CD，∴DE·DC＝AE·BD．
2、解：∵∠CDA=∠ADB=∠CDB， ∴ ∠CDA=∠ADB=∠CDB=120°
∴∠ACD=180°-120°-∠CAD = 60°-∠CAD.
又∵∠CAB=60°， ∴∠BAD=60°-∠CAD.
∴∠ACD=∠BAD. ∴△ACD∽△BAD.
∴
. ∴
.
即线段DA是线段DB、DC的比例中项.
3、证明：∵EF⊥AC，BC⊥AC，∴EF∥BC．
∵AE=CE，∴AF=FB．∴CF=AF=FB．
∵∠AFE=∠GFB，∠AEF=∠GBF，∴△AEF∽△GBF．
∴
．∴
．
∴CF是EF与FG的比例中项．
4、证明:（1）
.
（2）∵
DG∥CF
∴ 
又 
∴ 
5、(1)解：△DEF∽△ABC，△BDE∽△CEF．
证明如下：∵AB=AC，DE=DF，∴
．
∵∠EDF=∠A，∴△DEF∽△ABC． ∴∠DEF=∠B=∠C．
∵∠BED+∠DEF=∠C+∠CFE，∴∠BED=∠CFE．∴△BDE∽△CEF．
（2）证明：∵△BDE∽△CEF，∴
．
∵△DEF∽△ABC，∴
． ∴．
6、证明:(1) ∵CE⊥BD ∴∠CED=90° 又 ∠BDC=60°∴∠ECD=30°
∴CD=2ED ∵CD=2DA ∴ED=DA
(2) ∵ED=DA ∴∠DEA=∠DAE
∵∠EDC=60° ∴∠EAD=∠DEA=30°
∵∠BAD=45° ∴∠EAB=15°
又∠BDC=∠DBA+∠BAD ∴∠DBA=15°
∴∠EAB=∠EBA
(3) ∵∠EAB=∠EBA ∴BE=AE
∵∠AED=∠ACE ∴△AED∽△ACE
∴
∴AE2=AD·AC 即BE2=AD·AC
7、解：（1）∠1=1500－β，∠2=300+β－α；
（2）①由β=∠2或∠1=∠CQP，解得α=300.
∴当β在许可范围内变化时，α=300总有△ABP∽△PCQ.
②由β=∠1或∠2=∠CQP，解得β=750.
∴当α在许可范围内变化时，β=750总有△ABP∽△QCP.
（3）可能.①α=300，β＝300；②β=750，α=52.50．