灵武英才学校八年级数学（上册）期末测试卷
（满分：120分 时间：120分 出卷人：杨子鸣）
卷首语：试卷分第Ⅰ卷和第Ⅱ卷。第Ⅰ卷考查基础知识与基本技能，分值为100分。第Ⅱ卷注重能力的考查，强调知识的理解与应用，分值为20分，第Ⅱ卷的题目又分A、B两个层次，选择不同层次的题目得到的分值是不同的，请根据自己的能力自主选择，第Ⅱ卷的总分值最高为20分，多做可以，但不得分。相信通过同学们的认真思考、细心解答，一定会取得较为满意的成绩，同时也能对本学期的学习情况做出评估。
第 Ⅰ 卷（100分）
一、填空题（共45分）
1、自主理解题（每空1分，共15分）
（1）写出三个无理数： 2 ， 0 ， 。
（2）写出三组勾股数： ， ， 。
（3）写出菱形的三条性质： ， ， 。
（4）写出平行四边形的三种判别方法： ，
， 。
（5）写一个图象经过第二、四象限的正比例函数： ；
写出一个y的值随x的值增大而减小的一次函数： ；
写出一个以x=2，y=3为解的二元一次方程： 。
2、“双基”考查题（每题2分，共30分）
（1）－27的立方根是 ，18的算术平方根是 。
（2）化简：
=
，
=
。
（3）比较大小：
，
5.6。
（4）图象经过点A（－2，6）的正比例函数的关系式为 。
（5）方程组
的解是
。
（6）八年级一班47名同学中，12岁的有5人，13岁的有27人，14岁的有12人，15岁的有3人，则这班同学的年龄的众数是 ，中位数是 。
（7）一个正多边形的每个内角都为135º，则这个多边形的内角和是 度。
姓名： 班级： 考号： 得分：
（8）将一条2㎝线段向右平移3㎝后，连接对应点得到的图形的周长是 ㎝。
（9）、某拖拉机的油箱有油100升，每工作1小时耗油8升，则油箱的剩余油量y（升）与工作时间x（时）间的函数关系式为 。
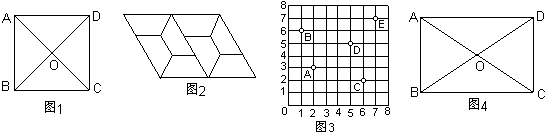
（10）如图1，正方形ABCD的对角线相交于点O，这个正方形可以看作由什么“基本图形” 经过怎样的变化形成的？ 。
（11）如图2是用形状、大小完全相同的等腰梯形密铺成的图案的一部分，这个图案中的等腰梯形的内角度数分别是 。
（12）如图3，若用（2，3）表示图上校门A的位置，则图书馆B的位置可表示为 ，（5，5）表示点 的位置。
（13）如图4，矩形ABCD的对角线AC、BD相交于点O，∠AOB=60º，AB=4㎝，则△AOB的形状是 三角形，AC长是 ㎝，BC长是 ㎝。
（14）小明从邮局买了面值50分和80分的邮票共9枚，花了6.3元。小明买了两种邮票各多少枚？
若设买了面值50分的邮票x枚，80分的邮票y枚，则可列出的方程组是 。
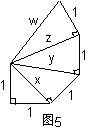
（15）根据图5填空：
x= ，y= ，z= ，w= 。
二、选择题（每小题3分，共15分）
1、下列不是中心对称图形的是（ ）
A、平行四边形 B、菱形 C、矩形 D、等腰梯形
2、平行四边形的周长为50，设它的长为x，宽为y，则y与x的函数关系为（ ）
A、y=25－x B、y=25+x C、y=50－x D、y=50+x
3、下列四点中，在函数y=3x+2的图象上的点是（ ）
A、（－1，1） B、（－1，－1） C、（2，0） D、（0，－1.5）
4、下列各式估算正确的是（ ）
A、
B、
C、
D、
5、下列说法中，正确的个数是（ ）
（1）只用一种图形能够密铺的有三角形、四边形、正六边形
（2）菱形的对角线互相垂直平分
（3）正比例函数y=kx（k≠0）的图象经过点（0，0）和（1，k）
（4）平移和旋转都不改变图形的大小和形状，只是位置发生了变化。
（5）一组对边平行，另一组对边相等的四边形是平行四边形
A、2个 B、3个 C、4个 D、5个
三、解答题（共40分）
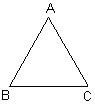1、（4分）如图是边长为4的正三角形ABC，建立适当的直角坐标系，写出各个顶点的坐标。
2、（4分）一个长度为5米的梯子的底端距离墙脚2米，这个梯子的顶端能达到4.5米的墙头吗？
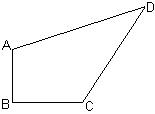3、（4分）如图，一块草坪的形状为四边形ABCD，其中∠B=90º，AB=3㎝，BC=4㎝，CD=12㎝，AD=13㎝，求这块草坪的面积。
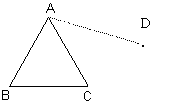4、（4分）（1）将正三角形ABC绕它的顶点C按顺时针方向旋转90º，作出旋转后的图形。（2）将正三角形ABC平移，使点A到D的位置。
5、（8分）分别用代入法、加减法解方程组
6、（6分）如图， AC//ED，点B在AC上，且AB=ED=BC，
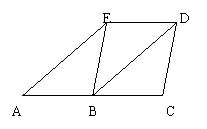写出图中的平行四边形，并说出理由。
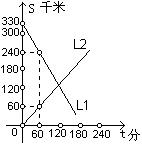7、（10分）A、B两辆汽车同时从相距330千米的甲、乙两地相向而行，s（千米）表示汽车与甲地的距离，t（分）表示汽车行驶的时间，如图，L1，L2分别表示两辆汽车的s与t的关系。
（1） L1表示哪辆汽车到甲地的距离与行驶时间的关系？
（2） 汽车B的速度是多少？
（3）求L1，L2分别表示的两辆汽车的s与t的关系式。
（4）2小时后，两车相距多少千米？
（5）行驶多长时间后，A、B两车相遇？
第 Ⅱ 卷（20分）（A组题）
1、（5分）今年我国遭受到“非典”灾难，全国人民万众一心，众志成城，抗击“非典”。图A-1是我市某中学“献爱心，抗非典”自愿捐款活动中，学生捐款情况制成的条形图，图A-2是该校学生人数比例分布图，该校共有学生1450人。
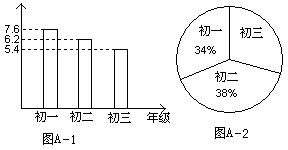(1)初三学生共捐款多少元？
(2)该校学生每人平均捐款多少元？
2、（6分）小明学完了“矩形”一节内容后，他想检验家中的门是不是矩形的，但他能利用的工具只的一个有刻度的20cm的直尺和一卷棉线。他能用这些工具检验吗？请你帮他设计一个检验的办法。（要求：方案设计合理，语言叙述清晰、流畅）
3、（9分）已知正比例函数y=k1x的图象与一次函数y=k2x－9的图象都经过点
P（3，－6）。
（1）求k1、k2的值。
（2）在同一直角坐标系中，画出这两个函数的图象。
（3）如果一次函数与x轴交于点A，求A点的坐标。
第 Ⅱ 卷（20分）（B组题）
1、（6分）某养鱼专业户年初在鱼塘中投放了500条草鱼苗，6个月后从中随机捞取17条草鱼，称重如下：
| 草鱼质量（千克） | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
| 草鱼数量（条） | 2 | 3 | 2 | 3 | 4 | 1 | 1 | 1 |
（1）求这些草鱼质量的众数与平均数（计算结果保留小数点后第2位）。
（2）估计这个鱼塘中年初投放的500条草鱼此时总质量大约有多少千克？
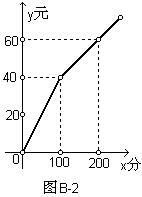2、（6分）移动公司为鼓励消费者，采用分段计费的方法来计算电话费，通话时间x（分）与相应的话费y（元）之间的函数的图象如图B-2所示。
（1）填空：月通话时间为100分时，应交话费 元；
（2）当x≥100时，求y与x之间的函数关系式；
（3）月通话时间为260分时，应交话费多少元？
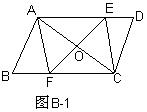3、（8分）如图B-1，平行四边形ABCD中，EF过AC的中点O，与边AD、BC分别相交于点E、F。
（1）试说明四边形AECF是平行四边形。
（2）若EF过AC的中点，且与AC垂直时，试说明四边形AECF是菱形。
（3）当EF与AC有怎样的数量和位置关系时，四边形AECF是矩形。