期末自我测评
一、填空题：（每题3分，共30分）
1．化简：
= ．（结果保留根号的形式）
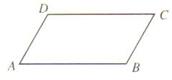2．如图，在□ABCD中，∠A=48°，BC=1㎝，则∠B= ，AD= ．
3．函数
的图像经过点(0, )与点(1, ).
4.如果四边形ABCD已经是一个平行四边形，那么再加上一些什么条件就可以变为正方形？ .
5.比较两个数的大小：
.
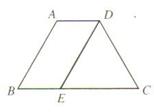
6.在等腰梯形ABCD中,∠C=60°,AD∥BC,DE∥AB,而且AD=2,BC=5,请求出AB= .
7.某大学采用了标准分计算方法作量化评估每一位学生的在校表现情况,总分和每个考核单项的满分都为100分,具体的计算方法是:学期综合测评成绩=学习平均成绩分×70﹪＋操行评估分×18﹪＋社会工作及活动评估分×12﹪.如果一个学生的学习成绩平均分、操行评估分、社会工作及活动评估分分别是91,95,83,那么这个学生的学期综合测评成绩是 .
8.如果A(2,-3),B(-4,-3)是平面直角坐标系上的两点,线段AB与y轴的位置关系是
.
9.如图,两个五角星构成一个中心对称图形,请指出它的对称中心是 ；点A的对称点是 ；点E是线段
的中点.
10.根据传说,古埃及曾用“拉绳”的方法画直角.现有一根长24厘米的绳子,请你也尝试着去做一做,利用它折出一个周长为24厘米的直角三角形.那么根据你的设想折出的直角三角形各边的长度分别是 厘米,其中的道理是 .
二、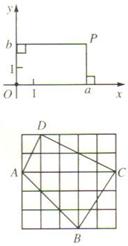
选择题：(每题4分，共16分)
11.9的算术平方根是( ).
(A)
(B)± (C)3
(D)±3
12.如图,在平面直角坐标系中,P点的坐标可以记为( ).
(A)P(a,b) (B)P(b,a) (C)P(-a,-b) (D)P(-b,-a)
13.如图,小方格都是边长为1的正方形,则四边形ABCD的面积是( ).
(A)25 (B)12.5 (C)9 (D)8.5
14.在一次函数y=4x＋3中,y的值随x值的增大而( ).
(A)增大 (B)减小 (C)先增大,后减小 (D)无法判断
三、计算题：(每题5分，共10分)
15. 
.
16.解方程组
四、解答题：(共44分)
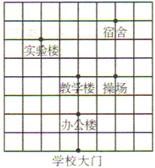
17.(8分)如图是某学校的平面示意图,你能否用适当的直角坐标系描述各个地点的位置的坐标?
18.(8分)一家鞋店在一段时间内销售了某种品牌的女鞋30双,其中各种尺码的鞋的销量如下表所示：
| 鞋的尺码/厘米 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量/双 | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
(1)求出这30双女鞋的尺码的平均数、中位数和众数.
(2) 你认为以上哪个统计数据是是鞋店老板最感兴趣的？为什么？并给他一个较好的经营建议.
19.(8分)某船的载重量为260吨,容积为1000m3，现在甲、乙两种货物要运,其中甲种货物每吨体积为8m3,乙种货物每吨体积为2m3,若要充分利用这艘船的载重与容积,甲、乙两种货物应各装多少吨?(设装运货物时无任何空隙)
20.(10分)如图,AD是△ABC的角平分线,DE∥AC交AB于E点,DF∥AB交AC于F点.
(1)
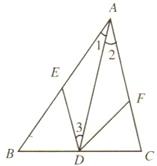∠1和∠2的大小有什么样的关系?
(2)四边形AEDF是菱形吗?如果是,请说明其中的道理.
21.(10分)小强和爷爷一起锻炼,主要活动是爬山.小强让爷爷先上,然后追赶爷爷.如图所示的两条线段分别表示爷爷和小强离开山脚的距离(米)与爬山所用的时间(分)之间的关系,而且是从小强开始爬山时计时.请看图回答问题：
(1)小强让爷爷先走了多少米?
(2)山顶高多少米?谁先爬到山顶?
(3)爷爷和小强爬到离山脚距离多少米处相遇?此时,小强用了多少时间?
(4)
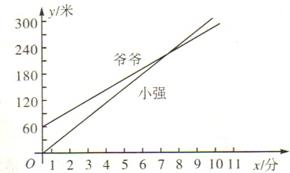爷爷的速度是多少?
(5)能否求出小强爬山的图象表达式?