| 学校： 班级： 座位： 姓名：
………………………………………装………………………………………订………………………………………线…………………………………… |
三溪片八年级数学期中试卷(2005.11)
一、选择题:(本题有8小题，每小题3分，共24分。)
1.
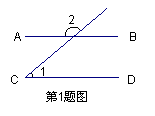
如图，已知：AB∥CD，若∠1＝50°，则∠2的度数是（ ）A、50° B、60° C、130 D、120°
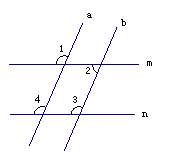
2.
如图，在下列条件中，能够直接判断
∥
的是（ ）A．∠1=∠4 B．∠3＝∠4 C．∠2+∠3＝180° D．∠1＝∠2
3. 已知等腰三角形一边是3，一边是6，则它的周长等于（ ）A．12 B．12 或15 C．15 D．18或15
4. 以下各组数据能作为直角三角形三边长的是 （ ）A、6，11，12 B、5，11，12 C、6，12，13 D、5，12，13
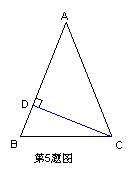
5. 如图，等腰三角形ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于A、44° B、68° C、46° D、22° ( )
6.
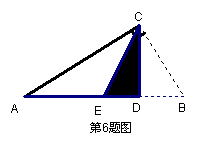
如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于
（
） A．25° B．30° C．45° D．60°
 |
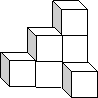
7. 
图1是小明用八块小正方体搭的积木，该几何体的俯视图是…………（
）
8. 下图可以沿线折叠成一个带数字的立方体，每三个带数字的面交于立方体的一个顶点，则相交于一个顶点的三个面上的数字之和最小是 （A） 7 （B） 8 （C） 9 （D） 10
二、填空题:(本题有6小题，每小题5分，共30分)
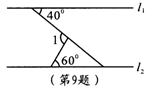
9.
如图所示，
，则
= 度。
10.
如图，请填上你认为适合的一个条件：
，能使AB∥CD
。
11. △ABC中，AB=AC, ∠A=36°，则∠B=____．
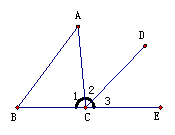
12. 如图,明明散步从A到B走了61米，从B到C走了60米，从A到C走了11米，则∠A+∠B的度数是_________
13. 等腰△ABC中，一腰AB的垂直平分线交另一腰AC于D，已知AB=12，△DBC的周长为20，则底边BC的长为（ ）.
 | |||
 | |||
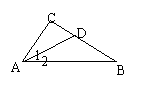14. 如图，△ABC中，∠C=90°，∠1=∠2，CD=5，BD=13，则AC= ．
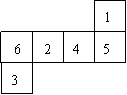
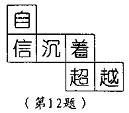
15. 一个正方体的每个面上都写有一个汉字，其平面展开图如图所示，那么在该正方体中，和“超”相对的字是 。
16.
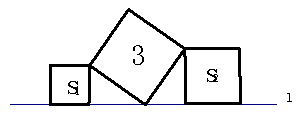在直线l上依次摆放着三个正方形(如图所示)。已知斜放置的已一个正方形的面积分别是3，正放置的两个正方形的面积依次是S1、S2，则S1＋S2＝_______。
三、解答题:(本题有7小题，共72分)
17. 正三角形给人以“稳如泰山”的美感，它具有独特的对称性，请你用三种不同的分割方法，将下列三个正三角形分别分割成四个等腰三角形。（在图中画出分割线，并标出必要的角的度数）（9分）
 | | |
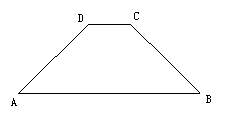
18. 如图，已知CD∥AB，∠A＝∠B，则∠C＝∠D，请说明理由。
 |
19.
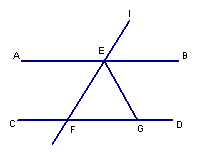直线
分别交AB、CD于点E、F，EG平分∠BEF，若∠EFG=40°，则∠EGF的度数是.
20. 已知一个几何体的三视图如图所示.请说出该物体的形状是什么?再画出它的表面展开图.
 |
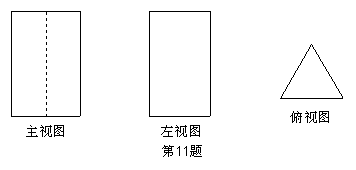21.
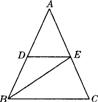如图，在△ABC中，AB=AC，BE平分∠ABC，DE∥BC． 求证：DE=EC
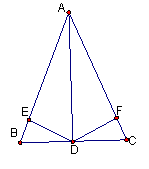
22. 如图，已知在△ABC中，AB=AC，D是BC的中点，DE⊥AB于E，DF⊥AC于F（1）证明：△BED≌△CFD（2）请你根据上述条件写出三个正确的结论。（不要求证明
23.
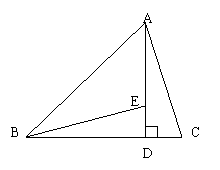如图，
中，
，
于
，点
在上
，且
，求证：
24. （5分）画出右图的三视图；
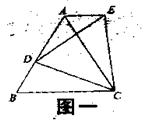
25. 如图一，等边△ABC中，D是AB上的动点，以CD为一边，向上作等边△EDC，连结AE。求证：AE//BC；
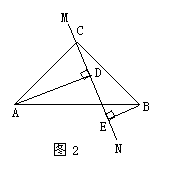
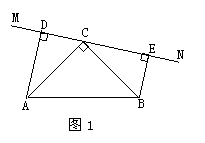
在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时，求证：
①△ADC≌△CEB；②DE=AD+BE；
(2)当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；
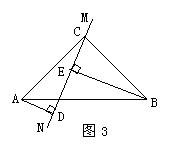
(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明.
 | |||
 | |||