期中考试复习
（90分钟，100分）
一、选择（每题3分，共30分）
1．下列变形中属于因式分解的是（ ）
2．2－a与3＋a同是（ ）的因式
A 
B 
C 
D
3．下列因式分解正确的是（ ）
A 
B 
C 
D 
4．三角形的外角和为（ ）
A360° B 270° C 180° D 90°
5．下列命题中，是假命题的是（ ）
A 等边三角形是等腰三角形 B 钝角三角形是斜三角形
C 等腰三角形是斜三角形 D 直角三角形不可能是等边三角形
6．△ABC中，∠A＝
∠B＝
∠C，则△ABC是（ ）三角形
A 锐角 B 钝角 C 直角 D 等腰三角形
7．三角形的一个外角小于它相邻的内角．这个三角形是（ ）
A 锐角三角形 B 直角三角形 C钝角三角形 D 不存在
8．三角形三条高线的交点一定在（ ）
A 三角形内部 B 三角形外部 C三角形内部或外部 D以上都不对
9．下列等式中正确的是（ ）
A 
B 
C 
D 
10．若分式
的值是1，则m的值为（ ）
A －2 B 3 C ＋2或－2 D 不存在
二、填空：（每空3分，共30分）
1．
__________
_______
2．当a_________时，
没有意义
3．若把
中的x和y的值都扩大到4倍，则分式的值_______________．
4．若
，则A＝_____________
5．等腰三角形的两边长2和5．则它的周长为__________
6．一个三角形的两边长为4和7，则第三边a的取值范围是_________，若第三边长为奇数，则第三边长为___________
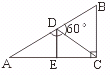
7．如图，∠ACB＝90°，∠ADC＝120°，D为AB的中点，且DE⊥AC，若CD＝5cm，则DE＝__________，BC＝___________
三、分解下列因式（每题4分，共20分）
1．
2．
3．
4．
5．
四、计算（每题5分，共10分）
1．
2．
五、求证：有两条高相等的三角形是等腰三角形（5分）
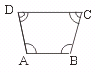
六、已知，如图，四边形ABCD中，AD＝BC，∠BAD＝∠ABC求证，∠ADC＝∠BCD（5分）
参考答案：
一、1．B
2．D 分析：
∴选D
3．C 4．A 5．D
6．B 分析：∠B＝3∠A、∠C＝5∠A 又∠A＋∠B＋∠C＝180° ∴∠A＋3∠A＋5∠A＝180° ∴9∠A＝180° ∠A＝20° ∴∠B＝60° ∠C＝100°
7．C 分析：则这个内角为钝角
8．D直角三角形三条高线一交点在形上．
9．B 分析：
C．
D．
10．B 分析：
∴3m＋2＝5m－4
∴2m＝6 ∴m＝3
二、1．
2．
， 分析：
，∴
3．不变 分析：
，不变
4．
，
分析：
5．12 分析：底边为2时，腰为5 ∴C
，底边为5时，腰为2与2．不能组成三角形．
6．3＜a＜11，5，7或9 分析：3＜a＜11 a＝5，7，9
7．DE＝2.5cm BC＝5cm
分析：D为AB中点心 ∴ DB＝DC，又∠ADC＝120° ∴∠BDC＝60°
∴∠B＝60° ∠A＝30° ∴ AD＝CD＝5cm，BC＝5cm，DE＝
三、1．原式＝
2．原式＝
3．原式＝
＝
4．原式＝
5．原式＝
四、1．原式＝
2．原式＝
五、已知：△ABC中，CE⊥AB于E．BD⊥AC于D且CE＝BD，求证，AB＝AC．
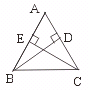
证明：在Rt△CBE与Rt△CBD中
∴ Rt△CBE≌Rt△CBD（HL）
∴ ∠EBC＝∠DCB ∴AB＝AC
六、证明，延长DA、CB相交于E
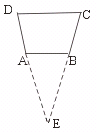
∵ ∠BAD＝∠ABC ∴ ∠EAB＝∠EBA
∴ AE＝BE ∴ AD＝BC ∴ DE＝EC ∴ ∠ADC＝∠BCD