2005年富阳市初二数学竞赛试卷

 一、选择题(每小题5分,共30分):
一、选择题(每小题5分,共30分):
1、若![]() 、
、![]() 、
、![]() 、
、![]() 都是有理数,并且
都是有理数,并且![]() ,
,![]() ,则
,则![]() 与
与![]() ( )
( )
A、互为倒数 B、互为负倒数 C、互为相反数 D、相等
2、已知![]() ,则
,则![]() 的取值范围是……………………………………( )
的取值范围是……………………………………( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]() 或
或![]()
3、设![]() 为
为![]() 的小数部分,
的小数部分,![]() 为
为![]() 的小数部分,则
的小数部分,则
![]() 的值为……………………………………………………………………………( )
的值为……………………………………………………………………………( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、在一次函数![]() 的图象上取一点P,作PA⊥
的图象上取一点P,作PA⊥![]() 轴,垂足为A,作PB⊥
轴,垂足为A,作PB⊥![]() 轴,垂足
轴,垂足
为B,且矩形OAPB的面积为![]() ,则这样的点P共有………………………………( )
,则这样的点P共有………………………………( )
A、4个 B、3个 C、2个 D、1个
5、已知不等边三角形中,有一条边长等于另两边长的平均值,则最大边上的高与最小边上的高的比值![]() 的取值范围是………………………………………………………………( )
的取值范围是………………………………………………………………( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、在边长为1的等边三角形内任意放一些点,要使得至少存在2个点之间的距离不超过![]() ,那么至少应该放几个点……………………………………………………………………( )
,那么至少应该放几个点……………………………………………………………………( )
A、![]() B、
B、![]() C、2
C、2![]() D、
D、![]()
二、填空题(每小题5分,共30分):
7、教室里共有8个人,每个人都和其余的每个人握一次手且只握一次手,则共握了 次手;
8、不论![]() 为何值,解析式
为何值,解析式![]() 表示的函数的图象经过一定点,则这个定点是 ;
表示的函数的图象经过一定点,则这个定点是 ;
9、甲、乙两人在环形跑道上练习长跑,甲的速度与乙的速度的比为5∶3,若两人同时从同一点出发,则乙跑了 圈后,甲比乙多跑了4圈。
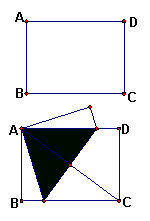 10、如图,矩形纸片ABCD中,AB=3
10、如图,矩形纸片ABCD中,AB=3![]() ,BC=4
,BC=4![]() ,
,
现将A、C重合,使纸片折叠压平,设折痕为EF,则
图形中重叠部分⊿AEF的面积为 ;
|
12、将![]() 分解因式
分解因式
|
三、解答题:
13、(10分)化简:![]()
14、(10分)已知三角形的一边是另一边的3倍,求证:三角形的最小边在周长的![]() 与
与![]() 之间。
之间。
15、(10分)当等腰三角形被一条直线分割成两个较小的三角形也是等腰三角形时,原等腰三角形的顶角度数是多少?这条直线怎样画?(讨论所有可能的解,并逐一画图表示)
16、(10分)两辆汽车从同一地点同时出发,沿同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆汽车前进60千米,两车都必须返回出发地点,但是可以不同时返回,也可以两车相互借用对方的汽油,为了使其中一辆车尽可能地远离出发点,另一辆车应当在离出发点多少千米的地方返回?离出发点远的那辆车一共行驶了多少千米?
初二数学竞赛参考答案
一、选择题(每小题5分,共30分):
1-6 CBABDA
二、填空题(每小题5分,共30分):
7、28 8、(2,3) 9、6 10、![]() 11、
11、![]()
12、![]() (注:分解一半给3分)
(注:分解一半给3分)
三、解答题:
13、解:设![]() ,则
,则![]() (
(![]() )…………………………3分
)…………………………3分
∴原式=![]()
=![]()
=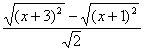
=![]() ……………………………………………………7分
……………………………………………………7分
∵![]() ≥0 ∴
≥0 ∴![]()
∴原式=![]() …………………………………………10分
…………………………………………10分
14、证明:设三角形一边为![]() ,另一边为
,另一边为![]() ,第三边的长为
,第三边的长为![]()
则第三边满足:![]() ………………………………………………3分
………………………………………………3分
所以边长为![]() 的边为最小边
的边为最小边
于是有 ![]() ……………………………………………6分
……………………………………………6分
即![]() 且
且![]() 即
即![]() <
<![]()
所以最小边在周长的![]() 与
与![]() 之间。 …………………………………………10分
之间。 …………………………………………10分
15、分两种情况讨论:
1、当直线通过等腰三角形的顶点时,有如左图的两个解:
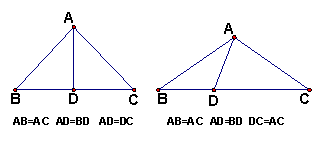 顶角:
顶角:![]() 、
、![]()
2、当直线通过等腰三角形的底角顶点时,有如右图的两个解。
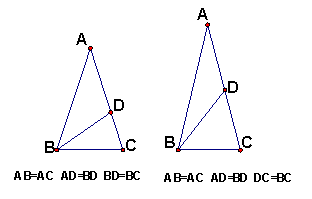 |
顶角:![]() 、
、![]()
注:本题评分按四个图形画出其中的两个按每个3分给分,画出第三、四个时每个2分。
16、解:设两辆汽车分别为甲、乙,并且甲用了![]() 桶汽油时返回,留下返程需要的
桶汽油时返回,留下返程需要的![]() 桶汽油,将多余的(24-
桶汽油,将多余的(24-![]() )桶汽油给乙,让乙继续前进,………………………………2分
)桶汽油给乙,让乙继续前进,………………………………2分
这时乙有:![]() 桶汽油,
桶汽油,
由题设:![]() ≤24 得:
≤24 得:![]() ≥8 ……………………………………5分
≥8 ……………………………………5分
甲、乙分手后,乙继续前进的路程是![]() 千米
千米
这说明当![]() 值越小时,代数式的值越大,………………………………………8分
值越小时,代数式的值越大,………………………………………8分
所以当![]() 时,得最大值480千米
时,得最大值480千米
因此,乙行驶的路程是2(60×8+480)=1920千米。…………………………10分