。11勾股定理
一．填空题
1．
如图在△ABC中，∠C=
，已知两直角边
A b C
a和b，求斜边c的关系式是__________________;
已知斜边c和一条直角边b（或a），求另一直角边 a
a（或b）的关系式是________________ c
或_______________.
B
2．在△ABC中，若
，则∠B+∠C=_____°.
3．在
△ABC中，∠C=,
若a=40，b=9，则c=__________;
若c=25，b=15，则a=________．
Ａ
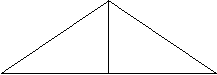
4．如图，△ABC中，AB=AC，
BC=16，高AD=6，则
腰长AB=________________.
Ｂ Ｄ Ｃ
第４题图
5．木工师傅做一个宽60
，高80的矩形木柜，为稳固起见，制作时需在对角顶点间加一根木条，则木条长为___________________.
6．一艘轮船以16
／
的速度离开港口向东北方向航行，另一艘轮船同时离开港口以12 ／的速度向东南方向航行，它们离开港口1小时后相距_________________.
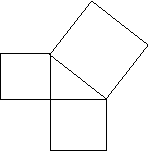7．如图，已知△ABC中，∠ACB=，
以△ABC各边为边向三角形外作三个正方形， Ａ 
、
、分别表示这三个正方形的面积，
=81，=225，则=__________________. Ｃ Ｂ
8．等腰三角形的腰长为13，底边上的高为5，则它的面积为_____________.
二．选择题
9．
在△ABC中，已知AB=12,AC=9,BC=15
则△ABC的面积等于
( )
A.108
B.54
C.180
D.90
1０．以下列各组数为三边的三角形中不是直角三角形的是 ( )
A．9、12、15 B．41、40、9 C．25、7、24 D．6、5、4
11．若直角三角形的两条直角边各扩大1倍,则其斜边扩大 ( )
A.
倍
B.1倍
C.2倍
D.倍
12．一个三角形三边之比为3∶4∶5,则这个三角形三边上的高之比为 ( )
A.3：4：5 B.5：4：3 C.20：15：12 D.10：8：2
13．
一个三角形的三边长为a、b、c,且满足等式
,则此三角形是
( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
14.
如图为求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使△ABC 恰好为直角三角形,且∠B=,测得AC=160米,BC=128米,则A、B两点间的距离为
( )
B
A．96米
B．100米
C．86米
D．90米
C A
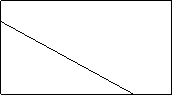15．如图，在一个长方形的
木块上截下一个三角形ＡＢＣ， A
使ＡＣ＝6cm，ＢＣ＝8cm，
截线ＡＢ的长是多少？ 6cm
C 8cm B
11勾股定理（2）
三．解答题
16．已知
、
、
是△ABC的三边，且
（
＞
且、 为自然数），△ABC是直角三角形吗？为什么？
４０
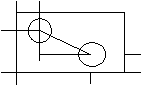17．在图中所示的长方形
零件示意图中，根据所给 Ａ
的部分尺寸，求两孔中心 ９０ Ｃ Ｂ
Ａ和Ｂ的距离（单位：
） ４０
１６０
18．小强到某海岛上去探宝，登陆后先往东走10千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到4千米处往东拐，仅走1千米便找到宝藏，问登陆点到宝藏埋藏点的直线距离是多少千米？
19．八（2）班数学课外活动小组的同学测量学校旗杆的高度时，发现升旗的绳子垂到地面要多1米，当他们把绳子的下端拉开5米后，发现下端刚好接触地面。你能将旗杆的高度求出来吗？
 |
20．在第六册课本的阅读材料中，介绍了一个第七届国际数学教育大会的会徽。它的主体图案是由一连串如图所示的直角三角形演化而成的.设其中的第一个直角三角形OA
=AA
=AA
=AA
=…=A
A
=1，请你先把图中其它8条线段的长的平方计算出来，填在下面的表格中，然后再计算这8条线段长的平方的乘积：___________________________.
|
|
|
|
|
|
|
|
|
21．如图是美国总统Ｇarfield于1876年给出的一种验证勾股定理的办法，你能利用它验证勾股定理吗？请做一做．
 |
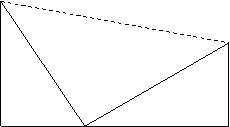b c c
a
a b
22．△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法中，错误的是 （ ）
A．如果∠C －∠B =∠A ，那么∠C =90° B．如果∠C =90°，那么
C．如果
，那么∠C =90° D．如果∠A=30°，那么AC
=3BC