勾股定理练习题

第一章《勾股定理》练习题

一、选择题（8×3′=24′）

1、在Rt△ABC中，∠C=90°，三边长分别为a、b、c，则下列结论中恒成立的是（　　） 　　　　　　　A、2ab<c²　B、2ab≥c²　　 C、2ab>c²　　 D、2ab≤c²

2、已知x、y为正数，且│x²-4│+（y²-3）²=0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（　　）　　　　　A、5　　　　　　　　　 B、25　　　　　 C、7　　　　　　　　　 D、15

3、直角三角形的一直角边长为12，另外两边之长为自然数，则满足要求的直角三角形共有（　　）　　 A、4个　　　　　　　B、5个　　　　C、6个　　　　　　　D、8个

4、下列命题①如果a、b、c为一组勾股数，那么4a、4b、4c仍是勾股数；②如果直角三角形的两边是3、4，那么斜边必是5；③如果一个三角形的三边是12、25、21，那么此三角形必是直角三角形；④一个等腰直角三角形的三边是a、b、c，（a>b=c），那么a²∶b²∶c²=2∶1∶1。其中正确的是（　　）

　　 A、①②　　　　　　　　 B、①③　　　　　　　　　　 C、①④　　　　　　　　　　D、②④

5、若△ABC的三边a、b、c满足a²+b²+c²+338=10a+24b+26c，则此△为（　　）

　　 A、锐角三角形　　 B、钝角三角形　　　　 C、直角三角形　　　　D、不能确定

6、已知等腰三角形的腰长为10，一腰上的高为6，则以底边为边长的正方形的面积为（　　）

　　 A、40　　　　　　　　　　 B、80　　　　　　　　　　　　 C、40或360　　　　　　D、80或360

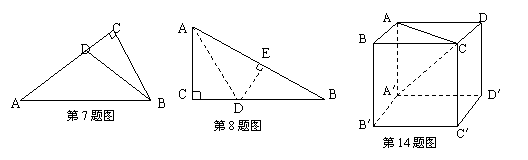
7、如图，在Rt△ABC中，∠C=90°，D为AC上一点，且DA=DB=5，又△DAB的面积为10，那么DC的长是（　　）

　　 A、4　　　　　　　　B、3　　　　　　　　　　C、5　　　　　　　　　　　　　D、4.5

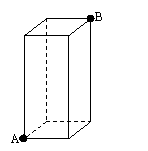
8、如图，一块直角三角形的纸片，两直角边AC=6㎝，BC=8㎝。现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（　　）

　　 A、2㎝　　　　 B、3㎝　　　 C、4㎝　　　　　 D、5㎝

二、填空题（12×3′=36′）

9、在△ABC中，点D为BC的中点，BD=3，AD=4，AB=5，则AC=___________。

10、在△ABC中，AB=AC，BD⊥AC于D，若BD=3，DC=1，则AD=____________。

11、在△ABC中，AB=2k，AC=2k-1，BC=3，当k=__________时，∠C=90°。

12、已知直角三角形的三边长为6、8、x，则以x为边的正方形的面积为_____。

13、已知直角三角形斜边长为12㎝，周长为30㎝，则此三角形的面积为____。

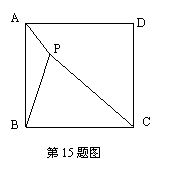
14、如图，正方形ABCD——A′B′C′D′的棱长为3，那么AC²=_______，A′C²=________。

15、如图，P为正方形ABCD内一点，PA=1，PB=2，PC=3，则∠APB=_______。

16、一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是_____________。

17、如图，每个小正方形的边长是1，在图中画出①一个面积是2的直角三角形；②一个面积是2的正方形。

18、把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边，如果要使三角形的面积是9㎝²，那么还要准备一根长为____的铁丝才能按要求把三角形做好。

19、将一根长为24㎝的筷子置于底面直径为5㎝，高为12㎝的圆柱形水杯中，设筷子露在杯子外面的长为h㎝，则h的取值范围是________________。

20、已知点P是边长为4的正方形ABCD的AD边上一点，AP=1，BE⊥PC于E，则BE=________。

三、解答题（6×10′=60′）

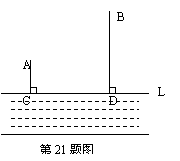21、如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？

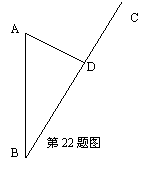22、如图，某沿海开放城市A接到台风警报，在该市正南方向260km的B处有一台风中心，沿BC方向以15km/h的速度向D移动，已知城市A到BC的距离AD=100km，那么台风中心经过多长时间从B点移到D点？如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险，正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？

23、数组3、4、5；5、12、13；7、24、25；9、40、41；……都是勾股数，若奇数n为直角三角形的一直角边，用含n的代数式表示斜边和另一直角边。并写出接下来的两组勾股数。

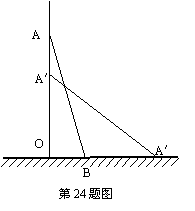24、一架方梯长25米，如图，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？（3）当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时，这时梯子的顶端距地面有多高？

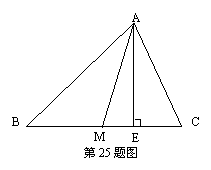25、如图，在△ABC中，AM是中线，AE为高线，证明：AB²+AC²=2（AM²+BM²）。

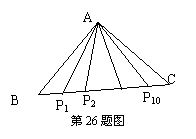26、如图，在△ABC中，AB=AC=2，在BC边上有10个不同的点P₁、P₂、…P₁₀，记M_i=AP_i²+P_iB·P_iC（i=1，2，…，10）。（1）求M_i的值。（2）求M₁+M₂+…+M₁₀的值。