大冶市2005年秋八年级数学期中测试卷
一、选择题：（12×3’＝36’）请将正确答案填入对应表格内
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、 下列各曲线中能表示y是x的函数的是
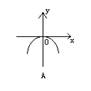
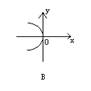
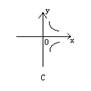
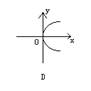
2、 下列一定能表示y是x的一次函数的是
A y＝kx+3 (k为常数) B y＝ +3 (k为常数, 且k≠0)
C y2＝x+3 D y＝ (k2+1)x+3 (k为常数)
3、
张洁把家中一个月的支出情况，用图中所示的统计图来表示，下面说法正确的是
A.从图中可以直接看出具体支出数额
B.从图中可以直接看出总支出数额
C.从图中可以直接看出各项支出数额占总支出的百分比
D.从图中可以直接看出各项支出数额在一月中的具体变化情况
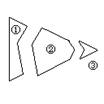
4、 如图，小明不小心把一块三角形的玻璃打碎成三块，他准备去配一块完全一样的玻璃，那么最省事的办法是
A．带① B．带② Ｃ．带③ Ｄ．带②和③
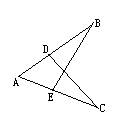
5、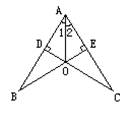 
如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1＝∠2，图中全等三角形共有
A．1对 B．２对 Ｃ．３对 Ｄ．４对
6、 函数y＝－x的图像，当x<0时在
Ａ．第一象限 Ｂ．第二、四象限 Ｃ．第二象限 Ｄ．第三象限
７、无论m为何值，直线y＝－2x＋m与y＝３x－１的交点不可能在
Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限 Ｄ．第四象限
8、已知函数y＝－x＋m与 y＝mx－4的图像的交点在x轴的负半轴上，则m的值为
Ａ．±2 Ｂ．±4 Ｃ．2 Ｄ．－2
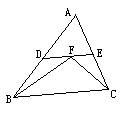
９、如图，Ｆ是△ＡＢＣ两内角平分线的交点，过点Ｆ作
ＤＥ∥ＢＣ交ＡＢ于Ｄ，交ＡＣ于Ｅ，则
Ａ．ＤＥ＝ＢＤ＋ＣＥ
Ｂ．DE＜BD＋CE Ｃ．DE＞BD＋CE Ｄ．无法确定
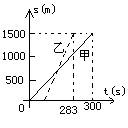
10、甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示（实线为甲，虚线为乙）小李根据图像得到如下四个信息，其中不正确的是
Ａ．这是一次1500米赛跑
Ｂ．甲、乙两人中先到达终点的是乙
Ｃ．甲、乙同时起跑
Ｄ．甲在这次赛跑中的速度为５m／s
11、如图，D在AB上，E在AC上，且∠B＝∠C，则补充下列一个条件后，仍无法判定△ABE≌△ACD的是
A．AD＝AE B．∠AEB＝∠ADC C．BE＝CD D．AB＝AC
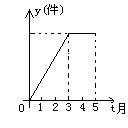12、某制衣厂今年前5个月生产衬衣的总量y（件）关于时间t（月）的函数关系的图象如图所示，下列说法正确的是：
A.1~3月每月生产总量逐月增加，4、5月每月生产总量逐月减少
B.1~3月每月生产总量逐月增加，4、5月每月生产总量与3月持平
C.1~3月每月生产总量逐月增加，4、5两月均停止生产
D.1~3月每月生产总量不变，4、5两月均停止生产
二、填空题（4’×7＝28’）
1、函数y＝ 中，自变量x的取值范围是__________
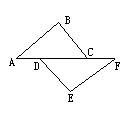2、如图，在△ABC和△FED中，AD＝FC，AB＝EF，当添加条件：
______________时，就可得△ABC≌△FED（只需填一个条件即可）
3、直线L与直线y＝2x+1的交点的横坐标为2，与直线y＝－3x+5无交点，则直线L的函数解析式为 __________
4、某市初中毕业、升学考试各学科及满分值情况如下表：
| 科目 | 语文 | 数学 | 英语 | 社会政治 | 自然科学 | 体育 |
| 满分值 | 150 | 150 | 120 | 100 | 200 | 30 |
若把该市初中毕业、升学考试各学科满分值比例绘成圆形统计图，则数学学科所在的扇形的圆心角是 度。
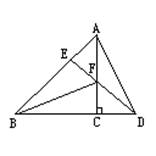
5、如图，在 △ABC中，∠B＝35o，∠C＝65o，D是BC上一点，DE⊥ AB于E，DF⊥AC于F，且DE＝DF, 则∠ADE等于
度。
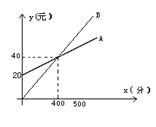6、一家电信公司给顾客提供两种上网收费方式：方式A收月基费20元，方式B不收月基费，一个月的上网费用y（元）与上网时间x（分）的函数关系如图，当上网时间为500分钟时，这两种方式上网费用相差
元。
7、国家规定个人发表文章，出版图书获得稿费纳税计算方法是：
(1) 稿费不高于800元的不纳税
(2) 稿费高于800元又不高于4000元的应缴纳超过800元那一部分稿费的14%的税
(3) 稿费高于4000元的应缴纳全部稿费11%的税。现在许老师获得一笔稿费，并缴纳个人所得税420元，问许老师这笔稿费有 元
三、解答题
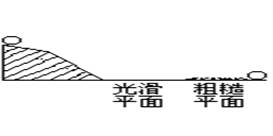
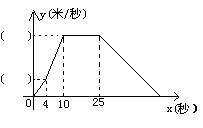
1．小明动手做实验，观察一个小球由静止开始滚动到结束运动的全过程。开始时小球在较缓的斜坡向下滚动，其速度每秒增加2米，4秒钟后，小球在较陡的斜坡向下滚动，速度变为每秒增加4米，后来小球在水平光滑的平面上做匀速直线运动，当小球到达粗糙不平的平面时，其速度每秒钟减少1米，最后停止下来。结合小球速度与时间的图象，回答下列问题：
（1）在y轴（ ）内填入相应的数值。
（2）小球从静止开始运动到停下来，共经过多少秒钟？
（3）求出当x≥25时，小球速度y（米/秒）与时间x（秒）之间的函数关系式。 （12’）
2．已知：如图，AB＝DE，BE＝CF，∠B＝∠DEF
求证：AC＝DF （10’）
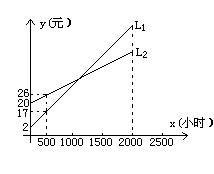
3．如图，L1，L2分别表示一种白炽灯和一种节能灯的费用y（费用＝灯的售价+电费，单位：元）与照明时间x（小时）的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样。
（1） 根据图象分别求出L1，L2的函数关系式。
（2） 当照时间为多少时，两钟灯的费用相等？
（3） 小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法。(直接给出答案不必写出解答过程) （12’）
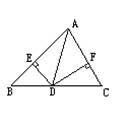
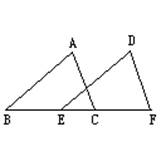
4．如图，△ABC中，AC＝BC，AC⊥BC，直线EF交AC于F，交AB于E，交BC的延长线于D，且CF＝CD，连结AD，BF。猜想BF与AD有何关系，并证明你的结论。 （10’）
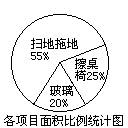
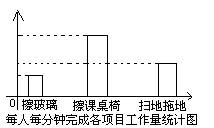
5．某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要完成总面积为80m2的三个项目的任务，三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示：
（1）从上述统计图中可知，每人每分钟能擦课桌椅__________m2；擦玻璃,擦课桌椅，扫地拖地的面积分别是__________m2, __________m2, __________m2,
（2）如果x人每分钟擦玻璃的面积是ym2，则y关于x的函数关系式是__________。
（3）他们一起完成扫地和拖地的任务后，把这13人分成两组，一组去擦玻璃，一组去擦课桌椅。如果你是卫生委员，该如何分配这两组的人数，才能最快地完成任务。 （12’）
数学参考答案
一、选择题
ADCAD CBDACBD
二、填空题
1. x＞5 2. AB∥EF 3. y＝－3x＋11 4. 72o 5. 50o 6. 5 7. 3800
三、解答题
(1) ① 8 32 ② 57秒 ③ y＝－x＋57
(2) 略
(3) ①y1＝0.03x＋2 (0≤x≤2000)
y2＝0.012x＋20 (0≤x≤2000)
②当y1=y2时，得x＝1000
③节能灯使用2000小时，白炽灯使用500小时
(4)①BF⊥AD ②BF＝AD 证明略
(5)① 16，20，44
②y＝ x
③8人擦玻璃，5人擦课桌椅